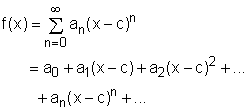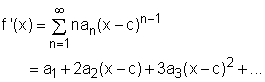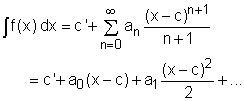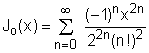| Ch 12. Infinite Sequences and Series | Multimedia Engineering Math | ||||||
|
Sequences and Series |
Integral and Comparison |
Alt. Series & Abs. Conv. |
Power Series |
Taylor, Mac. & Binomial |
|||
| Power Series | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Hengzhong Wen |
| Chean Chin Ngo |
| Meirong Huang |
| Kurt Gramoll |
| ©Kurt Gramoll |
| |
||
Power series, which are encountered often in science and engineering applications, will be presented in this section. An important function known as the Bessel function will also be discussed briefly. |
||
| Power Series |
||
A series of the following form
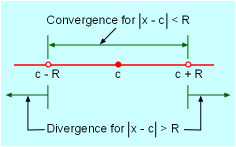
A power series can either converge or diverge for a given value of x. One can use the convergence testing methods introduced previously (e.g., ratio test and root test) to determine if a power series is convergent or divergent. The following theorem can also be applied to determine the convergence of a power series: |
||
|
For a given power series For example, the geometric series Σxn is
a special case of the power series (an = 1 for all n and c
= 0). It was shown previously that
this series is convergent when -1 < x < 1 and it is divergent when |
|
| Bessel Function |
||
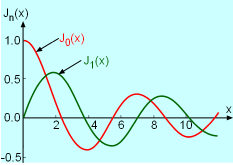 Bessel Function of Order 0 and 1 |
Power series is useful and important mainly because it can be used to represent functions arise in mathematics, science and engineering applications. One such function is called the Bessel function. The Bessel function of order 0 is defined by while the Bessel function of order 1 is defined as: |
|
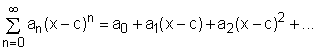
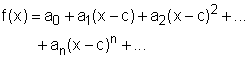
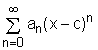 ,
only three possibilities exist:
,
only three possibilities exist: