| Ch 12. Infinite Sequences and Series | Multimedia Engineering Math | ||||||
|
Sequences and Series |
Integral and Comparison |
Alt. Series & Abs. Conv. |
Power Series |
Taylor, Mac. & Binomial |
|||
| Integral and Comparison Tests | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
The concept of series was
introduced in the previous section, and it is known that a series is
convergent when it has a finite sum. Two more convergence tests, the
integral test and the comparison test, will be presented in this section. |
||
| Integral Test |
||
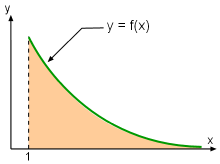 Improper Integral |
As mentioned in the previous section, the total sum of a series is often desired, but it is not trivial to obtain. The knowledge of whether a series is convergent or divergent becomes important since there is no point trying to determine the total sum of a series if it is a divergent series. The integral test is one of the methods which can be used to determine the convergence of a series, and it is stated as follows: Let f be a positive, continuous, and decreasing function on [1, (1) The series (2) The series Furthermore, if one uses a partial sum (Sn) to estimate the total sum (S) of a series using the integral test, the remainder Rn = S - Sn is given by These inequalities give a lower bound and upper bound for the estimation of the total sum of a given series. It is a common practice to take the midpoint of the interval for the approximation, and it provides a more accurate estimation. For example, take the series |
|
| Comparison Test |
||
The comparison test is another method to determine if a non-negative series is convergent or divergent. The basic idea of the comparison test is to compare a series with another series that is known to be convergent or divergent. The comparison test is formally stated as follows: Let Σan and Σbn be
series with positive terms. The above test is also referred to as the basic comparison test. Sometimes, the basic comparison test is difficult to apply. A more useful version is the limit comparison test, which is stated as follows: Let Σan and Σbn be
series with positive terms. |
||
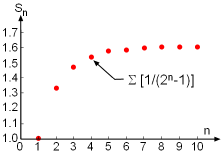 The Partial Sum of the Series Σ(2n - 1) Subject to Different n Values. |
Now, let's use the limit comparison test to determine if Let Hence, the given series is convergent. The partial sum of this given series subject to different n values is shown in the figure, and it confirms that the series is convergent. |
|
 (also
known as the p-series). Let f(x) = 1/xp, and it is a positive,
continuous and decreasing function. Applying the integral test to this
series yields
(also
known as the p-series). Let f(x) = 1/xp, and it is a positive,
continuous and decreasing function. Applying the integral test to this
series yields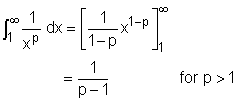
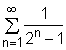 converges
or diverges.
converges
or diverges.