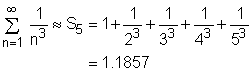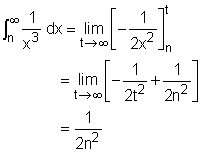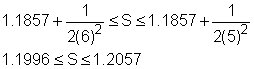| Ch 12. Infinite Sequences and Series | Multimedia Engineering Math | ||||||
|
Sequences and Series |
Integral and Comparison |
Alt. Series & Abs. Conv. |
Power Series |
Taylor, Mac. & Binomial |
|||
| Integral and Comparison Tests | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
Recall that the following inequalities, based on the integral test, give the lower and upper bounds for the approximation of the total sum: |
||
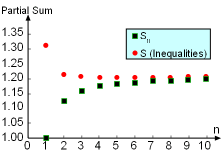 The Partial Sum S Based on the Inequalities and Sn Subject to Different n Vales for the Series Σ(1/n3) |
The improper integral can be evaluated as: The inequalities become Taking the midpoint as the total sum, hence Error = (1.2057 - 1.1996)/2 = 3.05 x 10-3 |
|