| Ch 11. Polar Coordinates | Multimedia Engineering Math | ||||||
|
Polar Coordinates |
Area and Length |
Conic Sections |
|||||
| Area and Length in Polar Coordinates | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
| Introduction |
||
|
|
In order to prepare for the Winter Olympics games, a ski resort is checking its slopes to make sure that they are compatible with Olympics standard. One of the ski tracks for the ski jump can be described using the function r = 100cos2θ meters for 0 ≤ θ ≤ π/2, as shown in the figure. The organizers of the games would like to find out what is the total length of the ski track. |
|
| Questions |
||
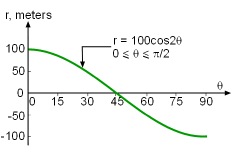 Estimated Curve for the Ski Track |
Determine the arc length of the polar curve. |
|
| Approach |
||
|
||
