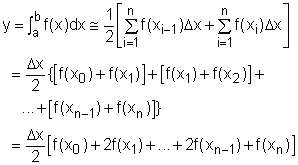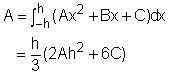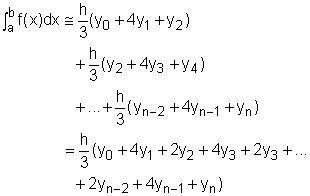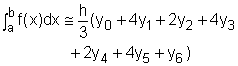| Ch 8. Integration Techniques | Multimedia Engineering Math | ||||||
|
Integration by Parts |
Trig. Integrals Trig. Subst. |
Fractions & Substitutions |
Approximate Integration |
||||
| Approximate Integration | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
In some situations, it is impossible to find the exact
value of a definite integral. For these cases, an approximate value of
definite integrals are needed. In this section, several rules to
find the approximate value of a definite integral are introduced. |
||
| Midpoint Rule |
||
|
|
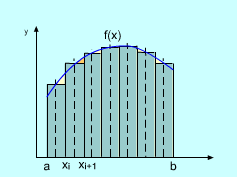
Since the definite integral is defined as a limit of Riemann sum, any Riemann sum could be used as an approximation to the integral. Recall, a definite integral is where f(x) is a continuous function on interval [a, b]. To apply an approximation, first divide the interval [a, b] into n subintervals of equal length Δx = (b - a)/n Next, choose a x in each subinterval and the integration can be approximated as where xi* is any point in the ith subinterval [xi-1,xi]. If xi* is choose to be the midpoint of each subinterval, this approximation is called the Midpoint Rule. xi* = 1/2(xi + xi+1) The definite integral of function f(x) in an interval [a, b] equals the area bounded by curve y = f(x), x = a, x = y, and y = 0. Therefore, Midpoint Rule actually is using a rectangle to approximate the area under the curve over a subinterval [xi-1 , xi]. |
|
| Trapezoidal Rule |
||
|
When using the Riemann sum to approximate definite
integration, the approximation is called left endpoint approximation
if the left point is choose as xi*. In the same
way, the approximation
is called right endpoint approximation if the right point is choose as
xi* . The Trapezoidal Rule is from
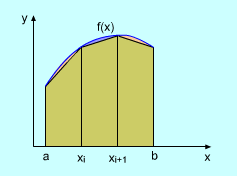
averaging these two approximation. Actually the Trapezoidal Rule is using a trapezoid to approximate the area over a subinterval. For example, in the interval [x0, x1], the area of the trapezoid is ΔA = Δx/2[f(x0) + f(x1)] When all the trapezoids at each interval are added together, the total gives, A = Δx/2[(f(x0) + f(x1))
+ (f(x1) + f(x2) + ... which is the Trapezoidal Rule approximation. |
|
| Simpson's Rule |
||
|
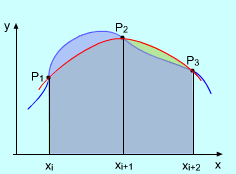
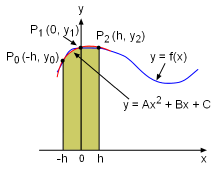
Simpson's Rule for approximation integration uses parabolas to approximate the curved edge. First divide interval [a, b] into n equal length subintervals h = Δx = (b - a)/n where n is an even number. On each consecutive pair of intervals, the curve y = f(x) can be approximated by a parabola y = Ax2 + Bx + C. To better understand this, consider a subinterval between x0 and x2. To simply the calculation, assume x0 = -h Then the area under the parabola is Since point P0, P1 , and P2 are on both curves, y0 = f(x0) = A(-h)2 - Bh + C Adding the above three equations together gives y0 + y1 + y2 = 2Ah2 + 3C Therefore, the area under the parabola can be rewritten as A = h/3( 2Ah2 + 6C) Shifting the parabola between [-h, h] to [x0, x2] does not change the area under it. Similarly, the area under the parabolas through point P2, P3, and P4 are A = h/3(y2 + 4y3 + y4) |
|
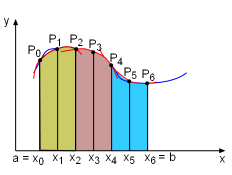 Simpson's Rule on Interval [a, b] (n = 6) |
Calculating the area under all the parabolas and adding them together gives If n = 6, the integration can be approximated as Note the pattern of coefficients is: 1, 2, 4, 2, 4, 2, ..., 4, 2, 4, 1. |
|