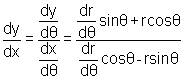Most of the discussion in this eBook has been given in terms of Cartesian coordinates (i.e., rectangular coordinates). The Cartesian coordinate system is set up such that the point of interest is given by distances relative from two perpendicular axes, generally labeled as x and y, as shown in the figure. In real world applications, sometimes it's convenient to use other coordinate systems. The polar coordinate system will be introduced in this section.

Polar Coordinate System

Examples: Point A, B and C in Polar Coordinates

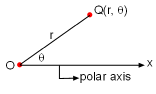
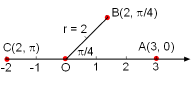
Let a point on a plane be the origin (or pole), denoted by the symbol O. A ray (half-line) originated from point O can be drawn, and it is called the polar axis. Normally, the polar axis is drawn horizontally to the right such that it corresponds to the positive direction of x-axis in Cartesian coordinates.

Let Q be another point on the same plane. The distance from O to Q is r and the angle between the polar axis and line OQ is θ. The angle is normally given in terms of radians. Positive angles are measured from the polar axis in the counterclockwise direction while negative angles are in the clockwise direction. Then the coordinates (r, θ) represents the polar coordinates of point Q. For example, point A in the figure is (3, 0), point B is (2, π/4) and point C is (2, π) when expressed in terms of polar coordinates.

Note that different polar coordinates may correspond to the same point. In general,

     Q(r, θ) = Q(r, θ + 2nπ) and
     Q(r, θ) = Q(-r, θ + (2n + 1)π)

where n is an integer.

Conversion between Cartesian
and Polar Coordinates

Examples: Polar Curves
r = 2 and θ = π/4

When the x-axis of the Cartesian coordinates coincides with the polar axis, the relationship between the Cartesian coordinates (x, y) and polar coordinates (r, θ) is given by

     x = rcosθ     and     y = rsinθ

To convert the Cartesian coordinates to polar coordinates, the following relationships are useful:

     r² = x² + y²     and     tanθ = y/x

Example: Cardioid (r = 1 + sinθ)

Example: Four-Leaved Rose (r = cos2θ)

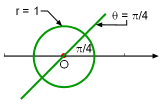
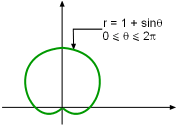
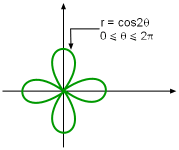
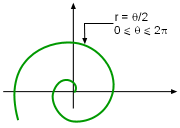
Some curves are more convenient to model in polar coordinates than in Cartesian coordinates. For example, r = 2 represents a circle with a radius 2. θ = π/4 represents a straight line as shown in the figure. Other examples of polar curves include a cardioid (r = 1 + sinθ), a four-leaved rose (r = cos2θ) and spirals (r = θ/2).

To take advantage of the symmetry, the following three rules are useful when sketching polar curves r = f(θ):

1. The curve is symmetric about the polar axis when f(θ) = f(-θ).
2. The curve is symmetric about the pole when the equation is unchanged by replacing r with -r.
3. The curve is symmetric about the vertical line
   (θ = π/2) when f(θ) = f(π - θ).

Example: Spirals (r = θ/2)

Tangent of a Polar Curve

When a curve is given in terms of polar coordinates r = f(θ), the equation can be rewritten in the parametric form as follows:

     x = rcosθ = f(θ)cosθ   and   y = rsinθ = f(θ)sinθ

where θ is the parameter.

According to the definition of the tangents introduced in the previous section, the tangents of the polar curve are defined as: