| Ch 9. Integrate Application | Multimedia Engineering Math | ||||||
|
Area Between Curves |
Volume | Work | Average Value | ||||
| Average Value of a Function | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
| Introduction |
||
|
|
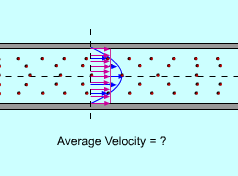
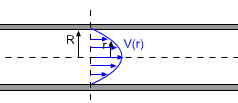
Amanda works at a biomedical engineering lab. For a particular project, a sensor needs to be installed in a blood vessel at a location where the blood velocity has the same magnitude as the average velocity of the whole vessel cross-sectional area. What is known:
|
|
| Questions |
||
|
||
| Approach |
||
Use the Mean Value Theorem for Integrals. |
||