| Ch 4. The Mean Value Theorem | Multimedia Engineering Math | ||||||
|
Maximum & Minimum |
Rolle's Theorem |
Mean Value Theorem |
Monotonic Functions |
First Derivative Test |
Concavity & Inflection |
Second Derivative Test |
|
| The Rolle's Theorem | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
In this section, Rolle's theorem is introduced along with three applications. |
||
| Rolle's Theorem
|
||
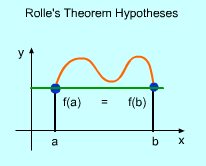 Rolle's theorem hypotheses
|
Rolles's theorem is used to find a function's horizontal tangent line. It is a special case of the mean value theorem which is discussed in the next section. Rolle's theorem states: If a function satisfies the following conditions
then there is a point between a and b such that its derivative is 0. This theorem can be better understood by examining the following cases:
|
|
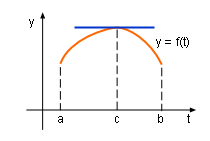 Velocity is 0 at the Point c |
|
|
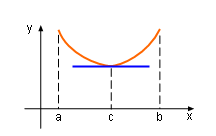 df(x)/dx = 0 at Point c |
|
|
 |
Notice that when a function satisfy Rolle's hypotheses, it may have multiple horizontal tangent line at various point when the function local extreme values are reached. | |