| Ch 4. The Mean Value Theorem | Multimedia Engineering Math | ||||||
|
Maximum & Minimum |
Rolle's Theorem |
Mean Value Theorem |
Monotonic Functions |
First Derivative Test |
Concavity & Inflection |
Second Derivative Test |
|
| The Rolle's Theorem | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
|
|
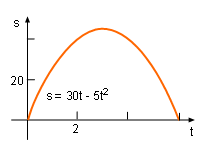
A ball is kicked directly upward. After the ball reaches its highest altitude, it falls back down to its initial position because of gravity. The altitude function of the ball is s = 30t - 5t2. How high can the ball go up? The for displacement and velocity units are m and m/s, respectively. Since the ball starts and ends at the same vertical location, its displacement function is continuous and differentiable. This satisfies the prerequisite of Rolle's Theorem, and thus a point exists so that the derivative with respect to time, t, is 0. ds/dt = d(30t -5t2)dt = d(30t)/dt - d(5t2)/dt = 30 - 10t As mentioned this must equal zero, ds/dt = 30 - 10t = 0 Since the derivative of displacement with respect to time is velocity, the above equation can be rewritten as ds/dt = v = 30 - 10t = 0 Therefore, t = 3 Substituting t = 3 into the displacement function = 30(3) - 5(3)2 = 45 m Thus, the maximum altitude of the ball will be 45 m. |
|