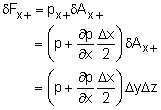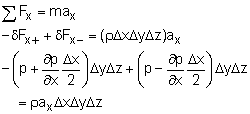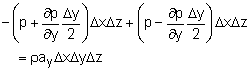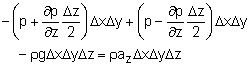| Ch 2. Fluid Statics | Multimedia Engineering Fluids | ||||||
|
Pressure Variation |
Pressure Measurement |
Hydrostatic Force(Plane) |
Hydrostatic Force(Curved) |
Buoyancy | |||
| Pressure Variation in a Static Fluid | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
|||||
| In this section, attention is focused on
the discussion of a fluid at rest or moving in a way such
that there is no presence of shearing stresses. The variations of pressure
with direction and depth in a fluid will be examined. |
|||||
| Pressure at a Point |
|||||
|
|
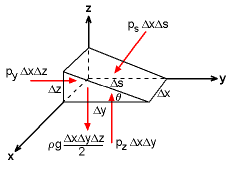
Consider a small triangular wedge of fluid taken from an arbitrary location within a fluid mass to determine the variation of pressure with direction. With the absence of shear stresses, the only forces acting on the fluid element are the normal and gravitational forces. Note that the forces in the x direction are not shown for clarity. According to Newton’s second law, the forces in the y and z directions can be summed as y-direction: pz - ps = ρ (Δz/2) (g + az) By shrinking the fluid element to a point, i.e., Δx, Δy, and Δz approach zero, it can be seen that py = pz = ps These results are known as Pascal’s law, which states that the pressure at a point in a static fluid is independent of direction. In other words, pressure is a scalar for fluids. |
||||
| Pressure Field |
|||||
|
|
Next, consider a small rectangular fluid element taken from an arbitrary location within a fluid mass. Let the pressure at the center of the element be p. Then, use the first order Taylor series expansion to determine the forces at the faces of the fluid element (forces in the x-direction are not shown for clarity). For the force at the x+ face: By assuming the only body force acting on the fluid element is due to
gravity (i.e., the weight of the fluid element) and the
absence of shearing forces (i.e., inviscid assumption), then applying
Newton’s
second law in the x-direction and yields |
||||
Similarly, according to Newton's second law, the force balances in the
y- and z- directions are given by The above equations can be simplified to obtain x-direction: These equations can be recast into vector notation: |
|||||
| Pressure Variation in a Static Fluid |
|||||
|
For a fluid at rest (i.e., Hence, it can be concluded that p varies only in the z-direction
and is not a function of x and y, giving |
||||
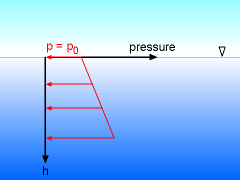 Hydrostatic Pressure Distribution in a Static Fluid |
Thus, pressure increases with depth in a linear fashion. This type of pressure distribution is called hydrostatic. We can also rearrange the above equation to yield an expression for the pressure head as follows: h = (p1 - p2) / ρg |
||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.