| Ch 2. Fluid Statics | Multimedia Engineering Fluids | ||||||
|
Pressure Variation |
Pressure Measurement |
Hydrostatic Force(Plane) |
Hydrostatic Force(Curved) |
Buoyancy | |||
| Pressure Variation in a Static Fluid | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Questions |
||
|
|
(a) Water towers in municipal distribution systems are often 100-125 ft in height. What pressure (psig) does this correspond to in the water pipes? (b) How far can the water level in the tank drop before the pressure
in the water main drops below 35 psig? (Note, this is often the minimum
design pressure.) |
|
| Solution |
||
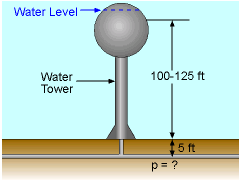 Problem Diagram for Part (a) |
(a) Assume static conditions (reasonable since water in the tanks moves very slowly). Also, assume the water mains are buried 5 ft below grade. For hydrostatic conditions, where γ = 62.4 lb/ft3 for water at 20 oC with H in ft, and p is in lb/ft2. Divide by 144 to get p in lb/in2 and the reference pressure is 0 atm (gage pressure), so p = (62.4 lb/ft3)(H ft)(1 ft2/144 in2) For H = 100 + 5 = 105 ft: p = 45.5 psig For H = 125 + 5 = 130 ft: p = 56.3 psig Hence, the pressure range is |
|
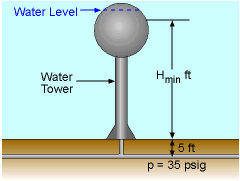 Problem Diagram for Part (b) |
(b) Find H if p = 35 psig. H = (35 psig)(144 in2/ft2) / 62.4 lb/ft3 = 80.8 ft Hence, the minimum water level in the tank is Hmin = 80.8 - 5 = 75.8 ft Note: 2.31 ft static water = 1 psig pressure, which is a good conversion factor to remember. |
|
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.
