| Ch 1. Basics | Multimedia Engineering Fluids | ||||||
|
Mass Density |
Ideal Gas Law |
Viscosity |
Surface Tension |
Vapor Pressure |
|||
| Mass Density and Specific Weight | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
In this section, mass density will be introduced.
The concept of the specific weight will also be presented. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Mass Density |
||||||||||||||||||||||||||||||||||||||||||||||||||||
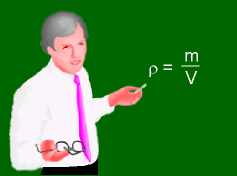 Mass Density
|
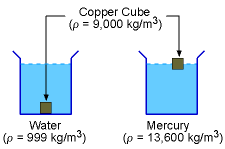
The mass density (ρ) of a fluid is defined as the ratio of the mass of the fluid (m) to its volume (V). That is, The SI unit for the mass density is kg/m3 while the English unit is slugs/ft3. For liquids, mass density is not a strong function of temperature and pressure. Hence, density is generally assumed to be independent of the temperature and pressure for liquids. On the other hand, for gases, density varies with both temperature and pressure. The relation between ρ, T and P for gases is given by the ideal gas law, which will be presented in a later section. The density of different liquids has a wide range. For example, the
density of water at 16oC is 999 kg/m3 while the
density of mercury at 20oC is 13,550 kg/m3. In
order for an object to float in a liquid, the density of the object must
be less than
that
of the liquid.
For example,
a copper cube (ρ = 9,000 kg/m3)
will sink in water but it will float on mercury. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
For gases, a similar phenomenon can be observed. Consider the balloons, as shown in the figure. The density of helium inside the balloons is less than the surrounding air for a given temperature and pressure, hence the balloons rise in air. For more information on this subject, readers are referred to the discussion of buoyancy. | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Specific Weight (or Weight Density) |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
The specific weight, γ, of a fluid is defined as where g is the gravitational acceleration. Basically, the specific weight represents weight per unit volume. Sometimes it is also referred to as the weight density. The SI unit for the specific weight is N/m3 while the English unit is lb/ft3. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Specific Gravity |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Specific gravity is simply the ratio of the specific weight of a given liquid to the specific weight of water at 4° C (γwater = 9.81 kN/m3 or 62.4 lb/ft3). This definition is helpful when comparing densities of different liquids. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.