| Ch 1. Basics | Multimedia Engineering Fluids | ||||||
|
Mass Density |
Ideal Gas Law |
Viscosity |
Surface Tension |
Vapor Pressure |
|||
| Viscosity | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Introduction |
||
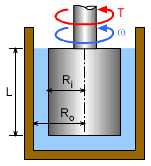 Rotational Cylindrical Viscometer |
Students are given a simple device called a rotational cylindrical viscometer, as shown in the figure, and asked to determine the viscosity of an unknown liquid. The outer cylinder is fixed while the inner cylinder is rotating at a constant angular speed of ω by applying a torque T. | |
| Questions |
||
Derive an equation for the viscosity in terms
of angular velocity, ω, torque, T,
submerged inner cylinder height, L, inner cylinder radius, Ri,
and outer cylinder radius, Ro.
Calculate the viscosity value when ω = 55 rev/min, T = 0.9 N-m, L = 0.3 m, Ri = 0.12 m and Ro = 0.13 m. |
||
| Approach |
||
|
|
|
|
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.