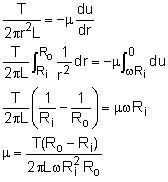| Ch 1. Basics | Multimedia Engineering Fluids | ||||||
|
Mass Density |
Ideal Gas Law |
Viscosity |
Surface Tension |
Vapor Pressure |
|||
| Viscosity | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
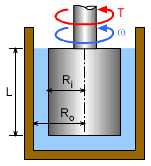
The liquid viscosity between the cylinder and container will resist motion. A high viscous liquid will require a high torque to keep it rotating. Thus, as expected, the viscosity of the liquid will be directly related to the torque needed to keep the cylinder rotating. First, define the toque in terms of the resisting force in the liquid. The torque is given by multiplying the force with its moment arm, T = Fr The force can be expressed in terms of the shear stress and area as follows: F = τ (2πrL) = T/r Rearrange terms to yield τ = T / 2πr2L According to Newton's law of viscosity for Newtonian fluids, τ = -μ du/dr |
|
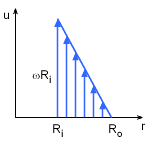 Velocity Profile of the Fluid between the Container and Cylinder |
The negative sign is inserted to indicate that u decreases as r increases. Note that the velocity profile is assumed to be linear, as shown in the figure. The end conditions are known and are given as u = ωRi at r = Ri and u = 0 at r = Ro. Equating the above two equations and integrating from For ω = 55 rev/min, T = 0.9 N-m, L = 0.3 m, Ri = 0.12m and Ro = 0.13 m, the viscosity of the liquid is calculated to be |
|
| If the gap between the wall and cylinder is small, then Ro - Ri => tgap, and Ri2 Ro => r3 where r is the mean radius. | ||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.