| Ch 1. Basics | Multimedia Engineering Fluids | ||||||
|
Mass Density |
Ideal Gas Law |
Viscosity |
Surface Tension |
Vapor Pressure |
|||
| Ideal Gas Law | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||||||||||||||||||||||||||
|
The ideal gas law will be introduced in this section. The conditions
in which the ideal gas law is valid will be examined through the compressibility
factor. |
||||||||||||||||||||||||||||||||
| Ideal Gas Law |
||||||||||||||||||||||||||||||||
|
Table: Gas Constant for Common Gases*
|
The relationship between pressure and temperature for most gases can be approximated by the ideal gas law, where p is the absolute pressure, V is the volume, m is the mass, T is the absolute temperature (units in Kelvin or Rankine) and R is the gas constant. Kelvin is related to Celsius by TK = TC + 273.15 and Rankine is related to Fahrenheit byTR = TF + 459.67. This equation is also referred to as the perfect gas law or the equation of state for an ideal gas. The gas constant R for some common gases is given in the table. Note that the density ρ is given by m/V, hence the ideal gas law can be written in terms of the density as p = ρRT The ideal gas law can also be written in per mole basis as follows: |
|||||||||||||||||||||||||||||||
| Compressibility Factor |
||||||||||||||||||||||||||||||||
Temperature for Various Gases*
|
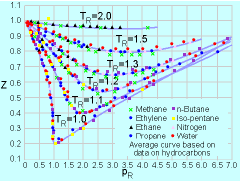
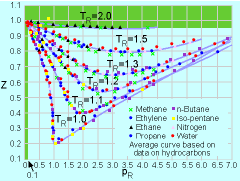
Having introduced the ideal gas law, the
next important question is: Under what conditions will the ideal gas
law be a good approximation
for real gases? To address this issue, the compressibility factor
Z is introduced, and it is defined as: pR = p/pc where pc and Tc are the critical pressure and critical temperature, respectively. The critical temperature is the maximum temperature that liquid and vapor phases can coexist in equilibrium. The corresponding pressure is the critical pressure. Values of critical pressure and temperature for some common gases are summarized in the table. From the compressibility chart, it is observed that Z approaches unity
when pR < 0.1 or TR > 2. Hence, these are
the conditions when the behavior of real gases can best be approximated
using the ideal gas law. * Source: Sonntag, R. E. and Borgnakke, C., "Introduction to Engineering Thermodynamics," John Wiley, Inc., New York, 2001. ** Reference: Su, G. J., "Modified Law of Corresponding States," Ind. Eng. Chem. (international ed.), Vol. 38, pp. 803, 1946. |
|||||||||||||||||||||||||||||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.