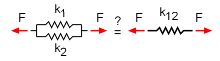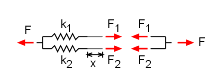| Ch 10. Vibrations | Multimedia Engineering Dynamics | ||||||
| Free Vibs. Undamped | Free Vibs. Damped | Forced Vibration | Energy Method | ||||
| Free Vibrations- Undamped | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||
| Harmonic Mass-Spring Motion |
||||||||
|
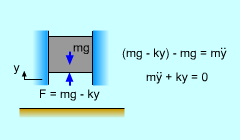
The simpliest type of vibrational motion is a mass moving back and forth horizontally due to a spring. To start the motion, the system is given either an initial displacement or velocity (or both). At any time, a force equilibrium and acceleration diagram can be constructed, similar to the diagram at the left. Summing forces in the x-direction gives, -Fs = m ax where Fs is the force in the spring, kx. This can be changed to, m d2x/dt2 + kx = 0 Because the basic differential equation describtion back and forth motion, it is refered to as harmonic motion. |
|||||||
 Vertical Mass-Spring Motion |
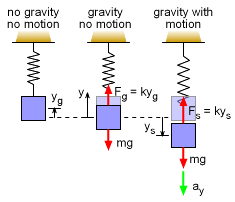
Similiarly, mass-spring motion in the vertical direction can also be modeled as a second order differential equation. Let the distance y represent the distance from the equilibrium position with gravity. The motion is started with an initial displacement and/or velocity. At any time, the forces can be summed, giving, FS - mg = -may But the FS is the spring constant times the total displacement, FS = k(yS + yg). Also, noting yS = y, the equation becomes, k(y + yg) - mg = -may However, ykg must equal 'mg' (see second graphic at left), and thus the 'mg' terms cancel, giving, m d2y/dt2 + ky = 0 which is the same as the horizontal equation. It is interesting to note, gravity does not effect the harmonic motion. |
|||||||
|
Using the vertical form of the differential equation, it can be written as where the term ωn is called the natural frequency, and is given by From differential equations, the general solution is y(t) = A sinωnt + B cosωnt where the constants A and B must be determined from the initial conditions of position and velocity. This general solution can be verified by substituting back into the differential solution and noting all terms cancel. Constant A is found by evaluating the initial condition dy(t)/dt at t = 0, |
|||||||
 Displacement Cycle over Time |
Constant B is found by evaluating y(t) at t = 0, B = y(0) The diagram at the left shows a typical response for a spring-mass system. Notice that the response y(t) oscillates about the equilibrium position sinusoidally with a constant amplitude. The frequency of oscillations, f, can be expressed in cycles per second (hertz) as The time taken to complete one full oscillation is called the period τ, |
|||||||
| Equivalent Springs (Series and Parallel) |
||||||||
Many times, there will be more than one spring. But the vibration equations developed above (and in next several sections) are for only one spring. With the concept of equivalent springs, all spring systems can be grouped into parallel and series springs which will have equivalent spring constants. |
||||||||
|
|
Parallel Springs If two springs are side-by-side, as shown in the diagram at the left, then the springs are in parallel. When parallel springs are stretched (or compressed) both springs will deflect the same amount, x. However, each spring can have a difference force, F1 and F2. F1 + F2 = F x k1 + x k2 = x k12 Canceling the deflection gives the equivalent relationship for two springs in parallel. |
|||||||
|
|
Series Springs Similar to two parallel springs, two springs in series can be reduced to a single equivalent spring constant, k12. When two springs in series are stretched (or compressed) the sum of the deflections in the two springs will equal the two deflection, x. x1 + x2 = x However, the force in each spring (and the total force) will be the same. F/k1 + F/k2 = F/k12 Canceling the force F, gives, |
|||||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.