| Ch 9. 3-D Motion of a Rigid Body | Multimedia Engineering Dynamics | ||||||
| Translating Coordinates | Rotating Coordinates | Inertia & Ang. Momentum |
Equations of Motion |
||||
| 3-D Motion: Translating Coordinates | Case Intro | Theory | Case Solution |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
Until now we have dealt only with the two dimensional motion of rigid bodies. For many applications, such as the dynamics of an airplane, motion in three dimensions needs to be modeled and analyzed. |
|||||
| Finite Rotations |
|||||
|
|
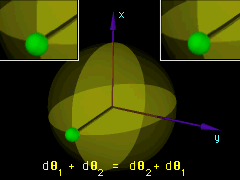
Although angular finite rotations have both magnitude and direction, they do not obey the rules of vector addition, and thus cannot be considered vectors. Δθx + Δθy ≠ Δθ y + Δθx However, rotations that are small (<1-2 degrees) in magnitude do obey the rules of vector addition, and thus are vectors. For example, consider small rotations of a sphere about its fixed central point 0. If the sphere undergoes two successive small rotations, the displacement dr of a point P on the surface of the sphere is independent of the order of the rotations: dr = dr1 + dr2 = dr2 + dr1 = dθ1 × r + dθ2 × r = dθ2 × r + dθ1 × r = (dθ1+ dθ2) × r = (dθ2 + dθ1) × r From this, we see that dθ1+ dθ2 = dθ2 + dθ1 |
||||
| Motion about a Fixed Point: Velocity |
|||||
|
|
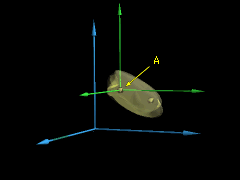
For a rigid body subjected to an angular rotation dθ, the angular velocity is defined by the time derivative ω = dθ/dt The line specifying the direction of ω is the instantaneous axis of rotation. For a body subjected to two component angular motions, ω1 and ω2, the resultant angular velocity is ω = ω1 + ω2. Once ω is specified, the velocity of any point rotating about a fixed point can be calculated as |
||||
|
|
|||||
| Body and Space Cone |
|||||
|
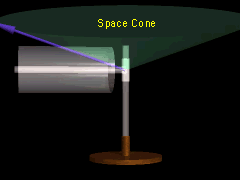
As the direction of ω changes, its axis traces a fixed space cone. If the change in the direction of this axis is viewed from the frame of the rotating body, the axis traces a body cone. |
|||||
| Motion about a Fixed Point: Acceleration |
|||||
|
The angular acceleration of a rigid body rotating about a fixed point is the time derivative of the angular velocity: α = dω/dt If ω and α are known, the acceleration of any point rotating about a fixed point can be obtained by differentiating the velocity with time: |
|||||
| Derivative of a Vector Measured from a Translating-Rotating to a Fixed System |
|||||
|
If a rigid body exhibits general motion in three dimensions, we must determine the relationship between the derivative of a vector in the frame of the rigid body and its derivative with respect to a stationary frame. Assume the vector A is an arbitrary vector in the frame of the moving xyz axes, A = Axi + Ayj + Azk It can be shown that the time derivative of A in the stationary frame of the XYZ axes is dA/dt = (dA/dt)xyz + (Ω × A) Since Ω is the angular velocity of the moving frame as measured from the stationary frame, and (dA/dt)xyz is the time derivative of A with respect to the moving frame, giving, (dA/dt)xyz = (dA/dt)xi + (dA/dt)yj + (dA/dt)zk The term (dA/dt)xyz is also commonly noted as (dA/dt)rel . |
|||||
| General Motion |
|||||
|
|
For convenience, use a translating coordinate system xyz to define the motion of a rigid body with respect to a fixed system XYZ. The body is translating and rotating relative to XYZ with an angular velocity ω and an angular acceleration α. The position vectors rA and rB specify the location of points A and B, which are both fixed to the body. The position of B with respect to A is given by rB/A. Since the body is rigid, the motion of B as measured from xyz is the same as the motion about a fixed point. The origin of the xyz axes is located at A. This coordinate system translates with the body, but does not rotate (Ω = 0). The velocity and acceleration of point B with respect to a stationary XYZ coordinate system are
Here, vA and aA are, respectively, the velocity and the acceleration of point A in relation to the stationary coordinate system. These two equations are the same as those used to describe general plane motion, but now α measures both the change in magnitude and direction of ω. |
||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.