| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| Rotating Coordinates: Acceleration | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
 Two Connected Bars |
Example |
|
|
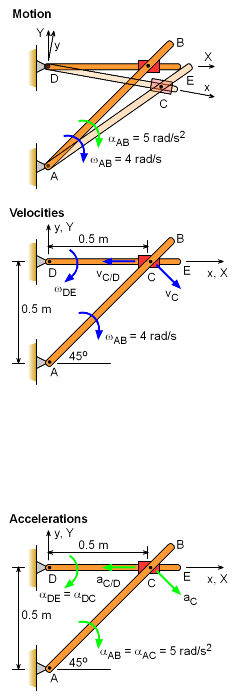
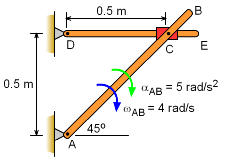
Two rods are pinned to a fixed point at one end, and connect to each other at the other end using a slider joint. Point C can freely move along rod DE but is pinned to rod AB at C. Rod AB rotates clockwise with angular velocity ωAB = 4 rad/s and angular acceleration αAB = 5 rad/s2 when θ = 45o. Find the angular acceleration of rod DE at this instant. The collar at C is pin connected to AB and slides over rod DE. |
||
| Solution |
||
|
|
Since the distance between point D and C varies, two frames of reference is useful to solve the problem. Attach the local x-y coordinate to the rotating AE rod, and the global X-Y coordinate to the non-moving background. Velocities: Putting all terms together gives, Acceleration of C can be determined from bar AC Putting all terms together gives, Comparing the j terms αDC = 11k rad/s2 (counter-clockwise) |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.