| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| Multiple Gears | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
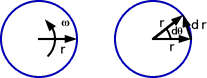
Gears are common in mechanical equipment and are used to transfer load and to change velocities. First, consider a point on a circular rotating body. The body rotates by dθ over time dt. The change in displacement is dr = r dθ By dividing by dt, the velocity of the point is dr/dt = r dθ/dt This can be written in vector form as v = ω × r The velocity direction is tangent to the circular path of point P. Since the velocity is always tangential to the radius, two touching objects will have identical velocities at the point of contact. Similarly, tangent accelerations are equal, but the normal accelerations are not. |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.