| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| Multiple Gears | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
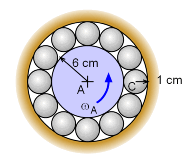 Rotating Shaft with Ball Bearings |
Example |
|
|
A cylindrical shaft is supported by spherical ball bearings that freely rotate. There is no slipping between the center cylinder and the bearings, or between the bearings and the outside surface. If the cylinder rotates at 4 rad/s, what is the velocity magnitude of a ball bearing center (point C)?
|
||
| Solution |
||
|
|
At any given instant, both points A and D are not moving. Thus, use those two points as pinned or fixed points (of course, an instant later, point D will be at a different location). Since there is no slipping, the velocity of point B will be the same on shaft or ball, thus, Now point C can be found by using the velocity of point D and B. |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.
