| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| Instant. Center of Zero Velocities | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
 Three Link Mechanism |
Example |
|
|
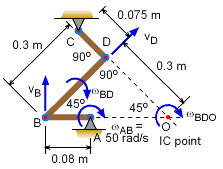
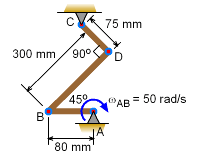
The rod AB rotates at ωAB= 50 rad/s about the fixed point A. The rod, CD is pinned at point C. Determine the angular velocity of the rod CD at the instant shown.
|
||
| Solution |
||
|
|
This could be solved using relative motion equations (vectors) as explained previous section, General Plane Motion: Velocities. However, for many velocity plane motion problems, using the instantaneous center of zero velocity (IC) can simplify the problem. The IC point will be at the intersection of the two lines perpendicular to the velocities of point B and D. For this instant, the triangle OBD is rotating about point O. The distances DO and BO are, The velocity of point B is, Thus, the angular velocity of BD is, The velocity of point D can now be determined, Finally, the angular velocity of CD is ωCD = 37.71 rad/s |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.