| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| Instant. Center of Zero Velocities | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Equations |
| Sections |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
||
|
|
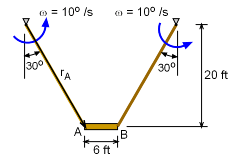
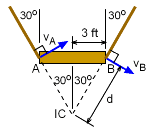
First, the velocity of points A and B can be easily determined by noting that the ropes rotate around a fixed point at the top of the building. Thus, the velocity at each point A and B on the work platform will be, |rA| = 20/cos30 = 23.09 ft ω = (10o/s)(π/180o) = 0.1745 rad/s |vA| = |vB| = ω rA = (0.1745) (23.09) = 4.029 ft/s The direction of each velocity is perpendicular to the rotating rope as shown in the figure. The Instantaneous Center of Zero Velocity (IC) is found by drawing perpendicular lines from both velocities. The IC point represents the pivot or rotation point for both velocities. Therefore, the the angular velocity of bar AB is v = ω d 4.03 = ω (3/sin30) ω = 0.672 rad/s = 38.5o/s It is interesting to note that the platform will rotate nearly four times as fast as the rope. The bottom line is that Jim Knowitall, the new window washer, will not be safe and will probably be thrown off the platform. |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.