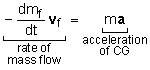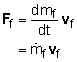| Ch 4. Particle Momentum and Impulse | Multimedia Engineering Dynamics | ||||||
| Impulse & Momentum | Consv. Linear Momentum | Impact |
Angular Momentum |
Mass Flow |
|||
| Mass Flow | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
 Conservation of Linear Momentum |
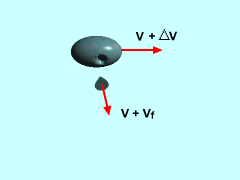
To understand mass flow problems, first consider an object of mass m and velocity v that ejects a small sub-element. Let the small element be mass Δmf with a velocity vf relative to the object. The the object's new velocity will be v + Δv. If a system containing the object and the element of mass is chosen such that no external forces act on it, then the total linear momentum must be conserved before and after the emission, giving
This simplifies to m Δv - Δmf Δv + mf Δvf = 0 The higher order term, Δmf Δv, will be very smaller when compared to the other terms due to the double delta. This term can be assumed to be zero. Now, assume that the object emits a continuous flow of mass Δmf during the period Δt. Divide by Δt, and take the limit as Δt approaches 0, |
||||
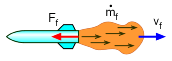 Force reaction is opposite to flow |
Comparing this equation with Newton's Second Law, it can be seen that a flow of mass from an object exerts a force on the object as
The force is proportional to the mass flow rate and the magnitude of the relative velocity of the flow. The direction of the force is opposite the direction of the flow. |
||||
| Conservation of Mass |
|||||
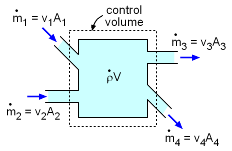 Conservation of Mass Example (dρ/dt) V = v1A1 + v2A2 - v3A3 - v4A4 |
While not a dynamics equation, the conservation of mass is a useful relationship in solving fluid problems. For a simple control volume, the mass change inside the volume must equal the difference of mass flow rate in and out of the volume. In equation form, where V (large V) is the volume. This can be simplified if the velocities (small v) and areas for each inlet and outlet or known, and there is no density change (dρ/dt = 0) in the control volume. Note, the mass flow for a given fluid, dm/dt is equal to the cross sectional area, A, and its velocity, v. This gives, These equations are simplifications of the full conservation of mass equations. Please refer to the Fluids Dynamics eBook for the complete equations. |
||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.