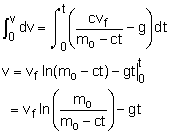Force and Acceleration Diagram
of Rocket

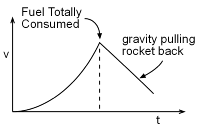
Use Newton's Second Law to sum all the forces acting on the rocket and equate it to the acceleration times mass,

     ΣF = ma

     F_f - mg = m (dv/dt)

The thrust, F_f, is due to the mass flow of the burning propellant. Using the mass flow equation gives,

     F_f = -(dm_f /dt) v_f = (dm_f /dt) v_fj = cv_fj

Notice, all motion and forces are only in the y direction. Combining equations for the y-direction,

     cv_f - mg = m (dv/dt)

Rearrange to get

     dv = (cv_f /m - g)dt

At any time t, the total mass of the rocket and the remaining fuel can be expressed as

     m = m_o - (dm_f /dt) t = m_o - ct

By substituting, the change in velocity, dv, is

Plot of Rocket Velocity Equation

Integration will give an expression for the velocity as

The total time required to burn all the fuel is

     m_f = (dm_f /dt)t_tot = c t_tot

     t_tot = m_f /c

Now that the time needed to burn all the fuel is known, it can be substituted back into the velocity equation to give,

where v_f = fuel velocity (constant)
         m_o = initial mass of rocket and fuel
         m_f = initial mass of fuel
         c = fuel burn rate, dm_f/dt