| Ch 4. Particle Momentum and Impulse | Multimedia Engineering Dynamics | ||||||
| Impulse & Momentum | Consv. Linear Momentum | Impact |
Angular Momentum |
Mass Flow |
|||
| Principle of Impulse and Momentum | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
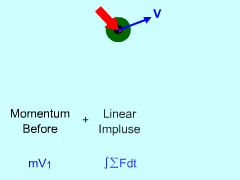 Change in Momentum |
Momentum reflects the tendency of a object to continue in the direction of its current velocity. To derive momentum and impulse, begin with Newton's Second Law ΣF = ma = m dv/dt and then integrate with respect to time, This equation may be easier to deal with if it is re-written as If this equation is analyzed using rectangular coordinates, it can be expressed as three scalar equations, These equations state that the impulse applied to an object equals its change in linear momentum. If the external forces acting on an object are known as a function of time, the change in velocity can be determined. |
||||
| Average Force |
|||||
|
In some cases it is easier to deal with the average force acting on an object, or only the average force is given. The average force applied from time t1 to t2 can be expressed as Using this expression for the average force with the previous momentum gives an expression for the change in velocity of an object in terms of the average force applied, This equation may also be expressed as three scalar equations, (t2 - t1) Fx-AV = mvx2 - mvx1 (t2 - t1) Fy-AV = mvy2 - mvy1 (t2 - t1) Fz-AV = mvz2 - mvz1 |
|||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.
