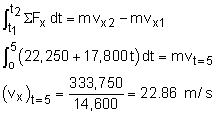| Ch 4. Particle Momentum and Impulse | Multimedia Engineering Dynamics | ||||||
| Impulse & Momentum | Consv. Linear Momentum | Impact |
Angular Momentum |
Mass Flow |
|||
| Principle of Impulse and Momentum | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Equations |
| Sections |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
||
| Solution of a) |
||
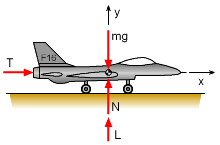 FBD of F-16 |
Because the takeoff roll is a straight line, this problem can be analyzed using rectangular coordinates. Begin with a free-body diagram. Let the origin of the rectangular coordinate system be located at the point where the plane begins the takeoff roll, with the positive x axis in the direction of the takeoff roll. Assume there is no force or velocity in the z direction. At t = 0, the velocity of the F-16 is 0, Use the value of the thrust at t = 0 and t = 5 to express the thrust in the x-direction during the first 5 seconds as a function of time, giving Tt=0 = 22,250i
N The velocity in the y direction is zero before take off and does not effect the velocity in the x direction. Likewise, forces in the y direction are independent of the thrust before take off. The change in momentum in the x direction is equal to the thrust impulse. This relationship can be used to determine the horizontal velocity for first 5 seconds, The total velocity after the first 5 seconds of the takeoff roll is |
|
| Solution of b) |
||
|
|
From t = 5 seconds to the time of liftoff (tLO), the thrust is constant and can be expressed as an average constant force, For an average or constant force, the impulse integral can be simplified to just force multiple the elapsed time. (t2 - t1) ΣFx-AV = mvx2 - mvx1 tLO = 8.00 s |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.