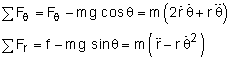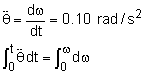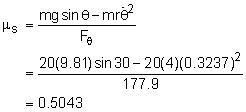| Ch 2. Particle Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Rect. Coord. |
Normal/Tang. Coord. |
Polar Coord. |
Orbital Mechanics | Computational Mechanics | |||
| Polar Coordinates | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
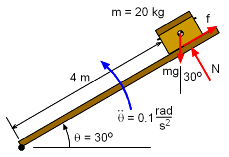 Force Diagram |
Begin with a free-body diagram at 30°. Sum the forces in both the radial and transverse directions. In the transverse direction, θ, there is only one unknowns, Fθ (= N). All other terms can be determined from the basic parameters given, mainly, r = 4 m Fθ = N = 20 (9.81) cos30 + 20 [ 0 + (4)(0.1) ] N = 177.9 N |
|
|
Now the second radial force equation can be used to find the minimum static coefficient of friction required to keep the chest from sliding when the drawbridge reaches an angle of 30°: The problem with this equation is dθ/dt is not known. To find it, the angular acceleration, a constant 0.1 rad/s2, needs to be integrated, ω(t) = 0.1 t = dθ/dt Now the problem is t is not known. By integrating it again, the angle, θ(t), can be determined, θ(t) = 0.05 t2 |
||
 Velocity Vector Animation
|
The time required for the drawbridge to reach an angle of 30° is θ(t) = 30o = 0.5237 rad = 0.1/2 t2 Substitute t back into the ω(t) equation above to determine the angular velocity of the drawbridge when it reaches an angle of 30°: ωt = 3.24 = 0.1 (3.236) = 0.3236 rad/s2 Now, that dθ/dt is known for 30°, the minimum static coefficient of friction is
|
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.