| Ch 1. Particle General Motion | Multimedia Engineering Dynamics | ||||||
|
Position, Vel & Accel. |
Accel. vary w/ Time |
Accel. Constant | Rect. Coordinates | Norm/Tang. Coordinates | Polar Coordinates |
Relative Motion |
|
| Curv. Motion: Normal/Tangential | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Solution of a) |
||
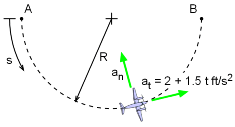
 Plane Path and Boundary Conditions |
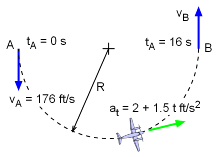
Since the velocity is tangent to the path, the rate of change of the speed is the tangential acceleration. at = dv/dt = 2 + 1.5t ft/s2 The tangential acceleration can be integrated to obtain an equation for the speed as a function of time. Since the plane enters the turn traveling at 176 ft/s, this becomes the lower limit of integration for the velocity, v = ds/dt = 0.75 t2 + 2 t + 176 Substituting the time required for the plane to complete the turn, the speed at B becomes vB = 0.75 (16)2 + 2 (16) + 176 = 400.0 ft/s |
|
| Solution of b) |
||
|
|
The velocity equation above can be integrated to obtain an equation for the displacement s as a function of time. s = 0.25 t3 + t2 + 176 t Again substituting the time required, the distance traveled during the turn is obtained as s = 0.25 (16)3 + (16)2 + 176 (16) = 4,096 ft Since the plane travels in a semicircular path and the total distance traveled is now known, the radius of of the path can be determined as R = 1,304 ft The radius of curvature is a constant equal to the radius of the semicircular flight path: ρ = R = 1,304 ft |
|
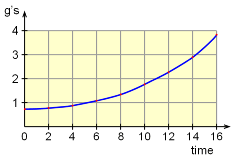 Acceleration in the Normal Direction over time (expresses as g's) |
The maximum centripetal acceleration occurs at point B, where the speed v is a maximum, an = v2/ρ = v2/R = 4002/1,304 = 122.7 ft/s2 The acceleration of gravity on Earth is constant at 32.2 ft/s2. At 122.7 ft/s2, the maximum centripetal acceleration that the plane experiences is approximately 4 times that due to gravity. It is unlikely that a cargo plane would execute such a "high-g" turn. |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.