| Ch 1. Particle General Motion | Multimedia Engineering Dynamics | ||||||
|
Position, Vel & Accel. |
Accel. vary w/ Time |
Accel. Constant | Rect. Coordinates | Norm/Tang. Coordinates | Polar Coordinates |
Relative Motion |
|
| Position, Velocity, Acceleration | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
 Toy Rocket |
Example |
|
|
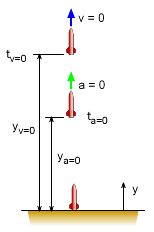
A small toy rocket follows a vertical path that can be modeled by y(t) = 5t3/6 - t4/12 (ft). What will be the maximum height? Also, what is the height when the acceleration is zero?
|
||
| Solution |
||
|
|
First, find the equation that models both the velocity and acceleration as function of time. v(t) = dx/dt = 5t2/2 - t3/3 a(t) = dv/dt = 5t - t2 a) The maximum height will occur when velocity is zero (it has reached it zenith). v = 0 = 5t2/2 - t3/3 Substitute time back into the position equation gives, yt=7.5 = 5 (7.5)3/6 - (7.5)4/12 b) Use the acceleration equation to find the time when the acceleration will be zero. a = 0 = 5t - t2 Substitute time back into the position equation gives, yt=5.0 = 5 (5)3/6 - (5)4/12 So, the rocket has a negative acceleration after the rocket goes up only 52.08 ft, but it keeps climbing until it reaches its zenith of 87.89 feet. |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.