| Ch 6. Rigid Body Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Moment of Inertia |
Translational Motion | Fixed Point Rotation |
General Plane Motion |
||||
| General Plane Motion | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Solution of a) |
||
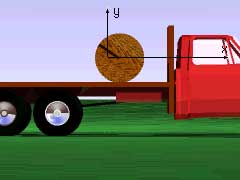
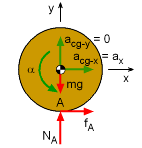 Problem Diagram
|
As with all dynamics problems, first start with a detailed diagram showing all forces and accelerations involved ( shown at the left). Summing the forces acting on the spool give ΣFx => fA = max ΣFy => NA - mg = 0 Since the spool rotates about its center of gravity, the moments are summed at the center, giving ΣMcg => fAr = Icg α There are four unknowns (fA, ax, NA, α) but only three equations. Thus, to complete the solution, a fourth equation must be derived that relates the acceleration of the spool's center of gravity to the angular acceleration. Because the spool does not slip, the acceleration of point A can be related to the acceleration of the cg point, acg = aA + acg/A |
|
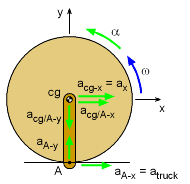 Acceleration Vectors for Link Between Points cg and A |
acg-xi + 0j = [aA-xi + aA-y j] + [acg-xi - acg-y j] axi + 0j = [atrucki + ω2r j] + [α r i - ω2r j]
ax = atruck - rα There are now four equations to solve for the four unknowns (fA, ax, NA, α). Combining gives two equations, (max) r = Icgα Reducing to one equation, mr (atruck - rα) = Icgα or α = m r atruck / [Icg + mr2] and ax = atruck - rα = 1 - 0.5(1.333) = 0.3333 m/s Thus, the spool accelerates to in the same direction as the truck acceleration even though it rolls backwards with an angular acceleration of 1.333 rad/s2. |
|
| Solution of b) |
||
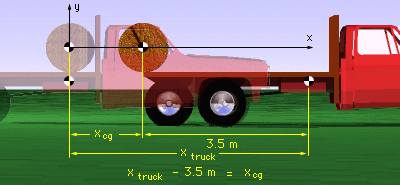 Position Diagram |
||
|
|
To determine the time it takes for the spool to reach the end of the truck, it helps to draw a diagram of the spool at the end of the truck. From the diagram, when the spool reaches the end of the truck, the following relationship is true, xtruck - 3.5 m = xcg Use the acceleration of the center of gravity of the spool and the acceleration of the truck to integrate to find xcg and xtruck, xcg(t) = 0.167 t2 xtruck(t) = 1/2 t2 Substituting the expressions for xcg and xtruck, gives 1/2 t2 - 3.5 = 0.167 t2 Solving for t, t = 3.24 s |
|