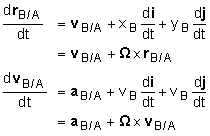| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| Rotating Coordinates: Acceleration | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
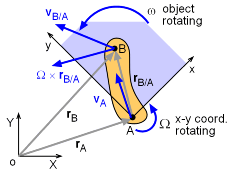
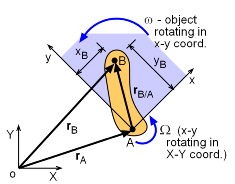 Position Vectors |
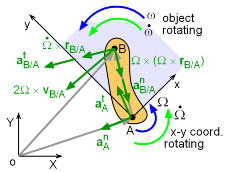
The acceleration of a moving point on a rotating rigid body is more complex than its velocity since there are tangent and normal terms. To determine the acceleration of a rotating rigid body with a moving point start with the relative velocity vector equation that was derived in the previous Rotating Coordinates:Velocities section. To help with modeling complex systems, two coordinate systems are used: X-Y is fixed and x-y rotates in the X-Y system. Note, x-y system is not fixed to the body. |
||||
|
|
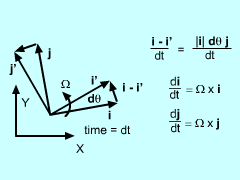
Start with the relative velocity equation for a moving frame of reference: vB = vA + Ω × rB/A + (vB/A)rel Differentiate with respect to time: aB = aA + dΩ/dt × rB/A + Ω × drB/A/dt + dvB/A/dt Similar to velocities, the x-y coordinate system is rotating inside the X-Y coordinate system. This means the time derivatives of the unit vectors, di/dt and dj/dt are not zero but di/dt
= Ω × i Thus, the time derivative of the position vector, rB/A is Putting all the terms together gives,
|
||||
| Coordinate Transformation |
|||||
Since two coordinates are involved with most rotating coordinate system problems, the two systems need to be related. In other words, one coordinate system needs to be mapped into the other, and vice versa. Relating two coordinate system is a common task in most all engineering fields, not just dynamics. |
|||||
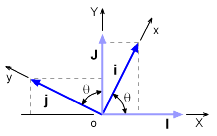 Velocity vectors |
The easiest way to relate coordinate systems is to describe one system in the other, just like is done for a point or vector. For example, the i unit-vector i can be described in the coordinate system XY as i = cosθ I + sinθ J likewise, the j unit-vector is j = -sinθ I + cosθ |
||||
These relationships can be inverted to describe I and J using i and j unit-vectors I = cosθ I - sinθ J |
|||||
These transformation equations are commonly written in matrix form, and called the 2D coordinate transformation matrix
They can be used for any two coordinate systems where the xy-system is rotated an angle θ relative to the XY-system. |
|||||