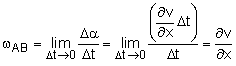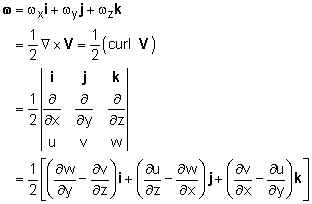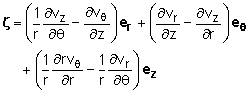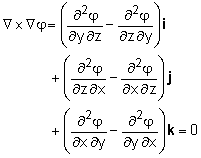| Ch 3. Fluid Kinematics | Multimedia Engineering Fluids | ||||||
|
Flow Descriptions |
Steady & Unsteady |
Streamlines, Streaklines |
Velocity & Acceleration |
Irrotational Flow |
|||
| Irrotational Flow | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||
|
In the previous section, velocity and acceleration of fluids was discussed. However, fluids can also rotate, which is referred to as vorticity. The concepts of both vorticity and velocity potential will be introduced. The definition of irrotational flow will then be given followed by a discussion of the potential flow. |
||||||
| Vorticity |
||||||
|
|
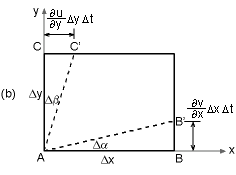
To develop an expression that models a rotating fluid element, consider an element under rotation over a small time interval Δt as shown in the diagram on the left. Notice, points B and C can move perpendicular to to the linear flow in the x and y directions, respectively. This is cause by rotating fluid. Over a given time span, point B and C will move, as shown. After a given time, Δt, line AB (AC will be similar) will rotate by angle Δα, giving where rotated angle Δα is assumed to be small. Next, the line AB will have an angular velocity, ωAB = Δα/Δt. Using Δα from above gives Similarly, the angular velocity of the line AC is given by The negative sign is introduced so that counter-clockwise rotation is taken to be positive. |
|||||
The total angular velocity, ωz, about point A, or the z-axis, is defined as the average of the angular velocity of two mutually perpendicular lines (i.e., line AB and AC). This gives Similarly, the angular velocity about the x- and y-axis are given by |
||||||
|
Then, the rotation vector (ω) is given by where the vector operation ( |
|||||
 Irrotational Flow |
When expressed in terms of polar coordinates, the vorticity is given by: A flow is said to be irrotational when there is no rotation of the fluid
elements. Hence mathematically, the flow is considered irrotational when
the vorticity or the curl of the velocity vanishes. That is, |
|||||
| Velocity Potential |
||||||
|
From vector calculus, it is known that the curl of any gradient must be zero, giving This is a math identity and has nothing to do with fluids. It is just a fact. It then must be true, that a velocity potential, φ, can be introduced for irrotational flow such that While this looks like just a mathematical game, it is actually very useful. The velocity potential function, a scalar, can be used to describe the velocity field and are related to the streamlines. |
|||||
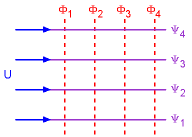 Equipotential Lines and Streamlines |
In Cartesian coordinates, the velocity components are related to the velocity potential as: In polar coordinates, they are given as: Constant φ lines are referred to as the equipotential lines, and they are orthogonal to the streamlines (constant stream function ψ lines) everywhere in the flow field as shown in the diagram at the left. |
|||||
| Potential Flow |
||||||
|
The concept of velocity potential is particularly useful when it is combined with the conservation of mass for incompressible fluids. For steady incompressible flow, the conservation of mass in vector form becomes the continuity equation, or simply If the incompressible flow is also irrotational, then the continuity equation can be written as The above equation is generally known as Laplace's equation, and this type of flow is referred to as potential flow. In Cartesian coordinates, the continuity equation can be expressed in terms of the velocity potential as follows: Some simple plane potential flows (e.g., uniform flow, source and sink, vortex and doublet) will be introduced in the Superposition of Flows section. |
||||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.