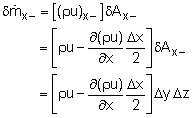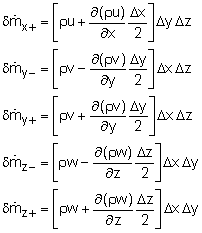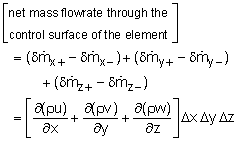| Ch 5. Fundamental Laws (Differential) | Multimedia Engineering Fluids | ||||||
|
Conservation Mass |
Navier-Stokes and Euler's |
Conservation Energy |
|||||
| Conservation of Mass | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
|||||
| The integral form of the continuity equation was developed in the Integral equations chapter. In this section, the differential form of the same continuity equation will be presented in both the Cartesian and cylindrical coordinate systems. The concept of stream function will also be introduced for two-dimensional , steady, incompressible flow fields. |
|||||
| Conservation of Mass (Continuity Equation):
Cartesian Coordinate System |
|||||
One should ask why is another form of the 'continuity equation' is needed. The previous form, the integral equation, work well when the integrands where know over the volume or surface. For problems with real defined volumes and known inflow and outflow, the integral form works well. On the other hand, if information is needed throughout the flow field, then a differential form is more useful. However, boundary conditions and initial conditions are needed to solve the differential form, which can be difficult. |
|||||
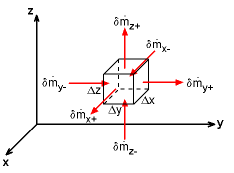
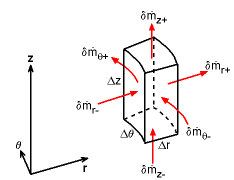
| According to the principle of conservation of mass, it is known that mass is conserved for a system. Consider a small differential element of fluid as shown in the figure. Let the density and velocities in the x-, y-, and z-directions at the center of the element be ρ, u, v and w, respectively. The mass flow rate at the faces of the differential element can then be obtained by using a first order Taylor series expansion. By neglecting higher order terms, the mass flow rate at the x-face is given as, | |||||
|
|
Similarly, the mass flow rates at other faces are given as, The net mass flow rate through the control surface of the small differential element is given by the difference between each parallel face, or The change of mass inside the differential element with respect to time is given by |
||||
Conservation of mass for the differential element in the Cartesian coordinate system can then be expressed as This equation is also commonly written in the following several forms, The term, If the flow is incompressible (i.e. constant density), then the material derivative of the density is zero (Dρ/dt = 0), and the conservation of mass equation becomes the continuity equation |
|||||
| Conservation of Mass and Continuity Equation: Cylindrical
Coordinate System |
|||||
|
Conservation of Mass for a Small Differential Element in Cylindrical Coordinate System |
By considering a small differential element as shown in the figure, a similar approach can be used to derive the conservation of mass equation for a cylindrical coordinate system. For brevity, the derivation steps are not repeated here. The conservation of mass equation expressed in cylindrical coordinates is given by Once again for steady flows, the equation is reduced to For incompressible flows, it becomes the continuity equation |
||||
| Stream Function |
|||||
|
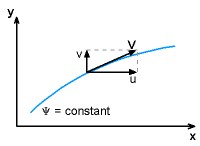
For two-dimensional, incompressible flows, the continuity equation in Cartesian coordinates is The partial differential equation still has two unknown functions, u and v. However, if a new stream function is arbitrarily defined as, then the 2D continuity equation becomes Thus, there exists a scalar function, ψ, that satisfies the continuity equation. This can now be combined with the vorticity equation and for irrotational flow (common), it can be shown that Notice, the new stream function, ψ, was just mathematically defined so that the number of unknowns (i.e., u and v) are reduced from two to one. This makes solving the 2D continuity equation easier, but it is now a second order differential equation. But there is a added benefit, the streamlines are lines where the stream function, ψ, is constant. |
||||
|
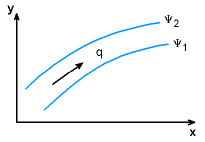
Recall, at every point in the flow field, streamlines are tangent to the velocity field. That is, dy/dx = v/u The value of the stream function associated with a particular streamline, ψ1 or ψ2, does not provide any useful information. However, the difference in the stream function values between any two closely-spaced streamlines (ψ2 - ψ1) will give the volumetric flow rate and indicate the flow direction. This is called a stream tube. That is, q = ψ2 - ψ1 For incompressible flow in the two-dimensional cylindrical coordinate system, the continuity equation is Similarly, the following stream function can be introduced to satisfy the continuity equation. |
||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.