| Ch 1. Basics | Multimedia Engineering Statics | ||||||
| Problem Solving | Units | ||||||
| Problem Solving & Significant Digits | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
|||||||||||||||||||||||||||||||||||||||||
| Introduction |
|||||||||||||||||||||||||||||||||||||||||
 Example of beam in equilibrium when forces are acting in multiple directions |
Welcome to Statics. For most engineering students this will be your first serious engineering class. Like most engineering classes, Statics relies on previous courses (math and physics) and will be used in future courses that you will take. Statics has all the basics of a regular engineering course, but is not too complex. The course revolves around just two equations, ΣF = 0 and ΣM = 0 Another way to think about these two main equations is that all forces (F) and moments (M) acting on a object must be in equilibrium. If this was not the case, then the object would move. In Statics it is assumed that nothing moves, but in Dynamics (the following course) this restriction is removed. Before solving actual statics problems, units, solution methods and significant digits need to be discussed. |
||||||||||||||||||||||||||||||||||||||||
| General Solution Procedure |
|||||||||||||||||||||||||||||||||||||||||
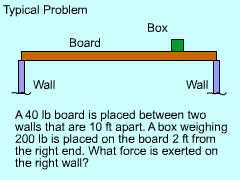 Example problem solved with solution steps |
The study of Statics involves only a few basic concepts and equations. The difficulty in statics is learning how to apply the equations to complex and different situations. In engineering, following a set procedure in solving problems saves time and decreases the number of errors. Generally, the following five steps will help solve problems in statics.
|
||||||||||||||||||||||||||||||||||||||||
| Fundamental Concepts |
|||||||||||||||||||||||||||||||||||||||||
As the name implies, Statics refers to the static equilibrium of all forces and moments acting on a body. This condition can be written in mathematical form as
While not all problems have both forces and moments in all three directions, both equations need to be satisfied in all three directions for the object to be in static equilibrium. Even though these two equations are simply, applying them to a particular structure can be difficult. Where are the forces, what are their directions, what is known, etc. become the main issues in the most Static problems. |
|||||||||||||||||||||||||||||||||||||||||
| Significant Digits |
|||||||||||||||||||||||||||||||||||||||||
|
In most engineering problems, there will be numerous intermediate steps and results. When writing down these intermediate results, it is important to use enough digits to minimize rounding errors. However, if too many digits are used, it takes a long time to write out the equations, and errors are easily made in keeping track of all numerical values. In general, numerical values can be rounded to four significant digits without loss of accuracy. Even using three digits is usually safe for most problems. However, round all numbers the same. If even one number is rounded to 2 significant digits and all the rest have four significant digits, the problem can still be off by a large amount (over 2%). Please note, significant digits is not quite the same as the just rounding decimal places. Significant digits are applicable to numbers both large and small whether nor not they have decimals. The table below shows a number of examples that illustrate that all numbers can be rounded to a given number of significant digits. Every number in the calculator should not be round just for the sake of rounding. Let the calculator keep all digits.
|
|||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
Practice Homework and Test problems now available in the 'Eng Statics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.