| Ch 3. Forces & Particle Equilibrium | Multimedia Engineering Statics | ||||||
|
Equilibrium and FBD |
2-D Forces |
3-D Forces |
|||||
| 2-D Forces (point) | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Example |
||
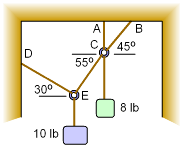 Two Hanging Weights |
Two boxes are hung from a ceiling and wall as shown in the diagram. Each box is supported by two cables that are interconnected through rings. What is the maximum tension in any rope other than the ropes directly connected to the boxes? |
|
| Solution |
||
In this example, there are two different loads that interact through a system of cables. Since all ropes are connected to at least one ring, it would seem reasonable to focus on the ring objects and make sure they are in static equilibrium. |
||
|
|
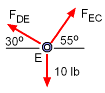
Drawing a free-body diagram of ring E, identifies two rope forces, FDE and FEC, that are not known. The direction of the loads are known since the force must act in the direction of the rope. The rope forces can be determined by applying force equilibrium in the x and y directions. ΣFx = 0 ΣFy = 0 Solving the two equations give, |
|
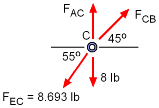 Free-body Diagrams of Ring C |
Now that the force in rope EC is know, ring C can be analyzed. Again, drawing a free-body diagram of ring C identifies two unknown forces, FAC and FCB. Applying the equilibrium equations gives, ΣFx = 0 ΣFy = 0 Maximum force occurs in rope AC, |
|