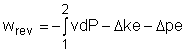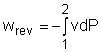| Ch 6. Entropy | Multimedia Engineering Thermodynamics | ||||||
| Entropy | Tds Relations |
Entropy Change |
Isentropic Process |
Isentropic Efficiency |
Entropy Balance (1) |
Entropy Balance (2) |
Reversible Work |
| Reversible Steady-flow Work | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Meirong Huang |
| Kurt Gramoll |
| ©Kurt Gramoll |
| |
||
| Reversible Steady-flow Work
|
||
|
|
The energy balance for a steady-flow device (nozzle, compressor, turbine and pump) with one inlet and one exit is: Its differential form is: δq - δw = dh + dke + dpe If the device undergoes an internally reversible process, the heat transfer term δq can be replaced by dh - vdP since δqrev = Tds Then the energy balance becomes dh - vdP - δwrev = dh + dke + dpe By rearranging the above equation, the reversible steady-flow work can be expressed as - δwrev = vdP + dke + dpe |
|
|
|
Integrating it form location 1 to location 2 yields, The above equation is the relation for the reversible work output associated with an internally reversible process in a steady-flow device. When the changes in kinetic and potential energies are negligible, the relation reduces to The above equation states that the larger the specific volume, the larger
the reversible work produced or consumed by a steady-flow device. To
minimize the work input during a compression process, one should keep
the specific volume of the working fluid as small as possible. In the
same manner, to maximize the work output during an expansion process, one should keep
the specific volume of the working fluid as large as possible. |
|
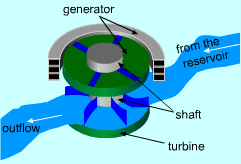 Power Generated by Hydraulic Turbine |
One needs to know the relationship between the specific volume v and the pressure P for the given process to perform the integration in the above relation. If an incompressible fluid is used as the working fluid, the specific volume v is a constant. The relation for the reversible work output associated with an internally reversible process in a steady-flow device is simplified to give wrev = -v(P2 - P1) - Δke - Δpe Hydraulic turbines used in hydroelectric power plants run in a steady-flow process with incompressible fluid, i.e., water, as the working fluid. |
|
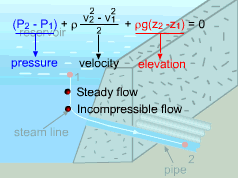 The Bernoulli Equation |
If no work interactions are involved, like nozzle or pipe section, the above equation is reduced to |
|
| Reversible Steady-flow Devices produce Most and
Consume Least
Work
|
||
 Reversible Turbine Delivers more Work than Actual Turbine |
The steady-flow devices deliver the most and consume the least work when it undergoes a reversible process. Consider two steady-flow devices, one is reversible and the other is irreversible (actual process), operating between the same inlet and exit states. The differential forms for the energy balance of these two devices are δqact - δwact = dh + dke + dpe δqrev - δwrev = dh + dke + dpe The right hand sides of these two equations are the same. It gives, qact - δwact = qrev - δwrev Rearranging this equation gives, δwrev - δwact = qrev - qact Since qrev = Tds, the above equation becomes, δwrev - δwact = Tds - qact the increase of entropy principle gives Thus, δwrev - δwact That is, for the same inlet and exit conditions, when the device undergoes a reversible process, a work-produce device like turbine produces the most work (w is positive), or a work-consuming device like compressor consumes the least work (w is negative). |
|