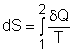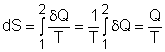| Ch 6. Entropy | Multimedia Engineering Thermodynamics | ||||||
| Entropy | Tds Relations |
Entropy Change |
Isentropic Process |
Isentropic Efficiency |
Entropy Balance (1) |
Entropy Balance (2) |
Reversible Work |
| Entropy | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
Refrigerant R-134a vaporizes in the evaporator and absorbs heat from the cooled space. Entropy changes
of the Refrigerant R-134a, the cooled space and the whole process need to be determined. |
|||||
|
Refrigerant R-134a enters the evaporator as a saturated liquid-vapor mixture and leaves the evaporator as saturated vapor. Hence the temperature in the evaporator remains constant at the saturation temperature of 200 kPa, which is, Tsat. @ 200 kPa = -10.09oC |
||||
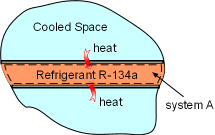 Heat Transferred into System A |
(1) Determine the entropy change of refrigerant R-134a Take refrigerant R-134a as a system (system A). It enters the evaporator as a saturated liquid-vapor mixture, which is state 1. P1 = 200 kPa Refrigerant R-134a leaves the evaporator as saturated vapor, which is state 2. P2 = 200 kPa During this process, refrigerant R-134 absorbs 150 kJ heat. Q = 150 kJ Hence, the entropy change for refrigerant R-134a from process 1-2 is Temperature T is a constant in this case, and the above equation can be integrated as Substituting Q and T into the above equation yields, ΔSA = 150(1000)/(-10.09 + 273) = 570.56 J/K |
||||
 Heat Transferred out of System B |
(2) Determine the entropy change of the cooled space Take the cooled space as a system (system B). During the heat transfer process, the space is maintained at -4oC and it dissipates 150 kJ heat to refrigerant R-134a. The entropy change of the cooled space can be determined as ΔSB =Q/T = -150(1000)/(-4 + 273) = -557.6 J/K |
||||
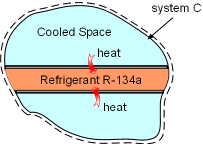 System C is an Isolated System |
(3) Determine the total entropy change of the process Take refrigerant R-134a and the cooled space together as a system (system C). Then refrigerant R-134a and the cooled space are subsystems of system C. The entropy change of system C is the sum of the entropy changes of its two subsystems. ΔSC = ΔSA+
ΔSB System C is an isolated system since no heat and mass transfer out of its boundaries. The entropy change of system C is greater than 0, which satisfies the increase of entropy principle. |
||||