| Ch 6. Structures | Multimedia Engineering Statics | ||||||
| 2-D Trusses: Joints | 2-D Trusses: Sections | 3-D Trusses | Frames and Machines | ||||
| 3-D Trusses/Space Trusses | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
 Example of Space Truss |
||
|
Similar to 2-D trusses, 3-D trusses (space trusses) require all members to have a pin joint at each end. Also, all loads must act at the joints. The above two conditions insure that member forces act in the direction of the members. Without knowing the direction of the load, truss problems could not be solved using just static equilibrium equations. |
||
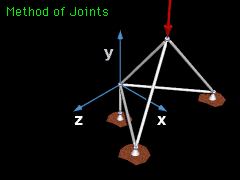
| Method of Joints |
||
|
|
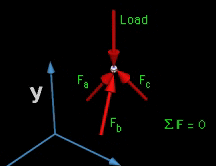
Space truss problems can be solved by choosing a joint with only three unknown member forces and one or more known load forces. The forces at the joint are summed in all three directions which will produce three equations and three unknowns. ΣFx = 0 ΣFy = 0 ΣFz = 0 The method of joints is usually the easiest method since the moment equilibrium equations are difficult to apply in 3D. Vector notation should be used with 3-D problems because of the complexity of 3-D geometry. |
|
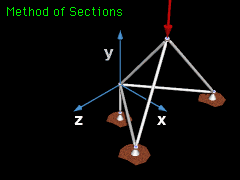
| Method of Sections |
||
|
|
If only a single-member load is needed, then the method of sections can be used, just like with 2D planar trusses. However, with 3D trusses, the section that is cut will have three moment equations in addition to the three force equations to find the unknowns. ΣFx = 0 ΣFy = 0 ΣFz = 0 ΣMx = 0 ΣMy = 0 ΣMz = 0 |
|
Practice Homework and Test problems now available in the 'Eng Statics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.