| Ch 7. Stress Analysis | Multimedia Engineering Mechanics | ||||||
|
Plane Stress |
Principal Stresses |
Mohr's Circle for Stress |
Failure |
Pressure Vessels |
|||
| Pressure Vessels | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
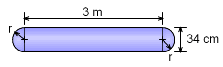
A gas storage tank needs to be designed to hold pressurized gas at 10 MPa. The tank inside diameter is set at 34 cm due to tank stacking system on a rail car. For safety reasons, a factor of safety of 2.0 is required. The material is steel with a yield stress of 250 MPa. The thickness of the material needs to be determined. To account for the stress interaction between the hoop and axial directions, the maximum distortion energy theory (von Mises' Yield Criterion) will be used to predict failure. It is assumed that the end caps will not fail and only the cylinder middle section will be considered (end cap stresses are complex and not studied in this eBook). |
|
| Hoop and Axial Stresses |
||
|
Functions for the hoop and axial stress can be determined for a cylindrical pressure vessel. These are σh = Pr/t = (10 MPa)(0.17 m)/t = 1.7/t σh = Pr/(2t) = (10 MPa)(0.17 m)/(2t) = 0.85/t Both the stresses are functions of t. |
||
| Failure Criteria |
||
 Stress Element at Cylinder Section |
The maximum distortion energy criteria takes into consideration stresses in multiple directions. The equation is or for this case, The yield stress is given as 250 MPa. However, to account for a factor of safety of 2.0, the actual yield stress is reduced in half. Substituting into the failure equation gives, 2.890 + 0.7225 - 1.445 = 15,625 t2 t = 0.1178 m = 11.78 mm |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.