| Ch 7. Stress Analysis | Multimedia Engineering Mechanics | ||||||
|
Plane Stress |
Principal Stresses |
Mohr's Circle for Stress |
Failure |
Pressure Vessels |
|||
| Mohr's Circle for Stress | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Equations |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
||
|
|
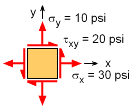
For a particular point in a structure, the local stresses were found to be 30 psi and 10 psi in the horizontal (x) and vertical (y) directions, respectively. The shear stress was found to be 20 psi. To help understand this stress state, a Mohr's circle will be constructed and used to find the 1) principal direction and principal stresses, 2) maximum shear stress direction and the maximum shear stress, and 3) the stress state if the element is rotated 15 degrees (counter-clockwise). |
|
| Basic Mohr's Circle |
||
 Basic Mohr Circle for Stress |
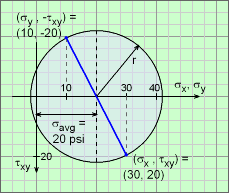
To construct a Mohr circle for a given stress state, first find the average normal stress, which will be the location of the circle's center. For this problem, it is σavg = (σx + σy)/2 = (30 + 10)/2 = 20 psi This value is plotted on the graph at the left. Remember, the average normal stress, σavg, is always on the horizontal axis. Next, at least one point on the circle's edge is needed to define the circle's radius. There are two points that can be found immediately without any calculation, (σx, τxy) or (σy, -τxy). Note that both σx and σy are plotted on the same horizontal axis. This may seem strange at first, but it works well since they are both normal stresses. Generally, a line is drawn between the two points and the center. All three should be in a straight line. If they are not, this is an early indication something is wrong. The circle radius can be determined by using the right triangle with vertices (20, 0), (30, 0) and (30, 20). |
|
| Principal Direction and Principal Stresses |
||
 Principal Stresses and Direction |
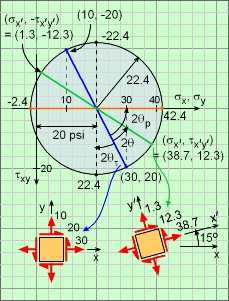
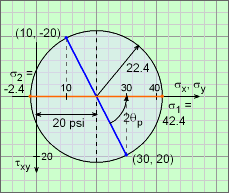
The principal direction is where the normal stresses, σx and σy are at a maximum or minimum. This condition is represented by the intersection of the circle and the horizontal axis (shown in the diagram as a orange line). To get to this condition, the current stress state (blue line), needs to be rotated to the horizontal by an angle of 2θp in the counter-clockwise direction. Using geometry in the diagram, this gives tan(2θp) = 20/(30 - 20) = 2 θp = 31.72o The actual principal stresses can be found using the circle center and the radius. They are, σ1 = σavg + r = 20 + 22.36 = 42.36 psi σ2 = σavg - r = 20 - 22.36 = -2.36 psi |
|
| Maximum Shear Stress Direction and Maximum Shear Stress |
||
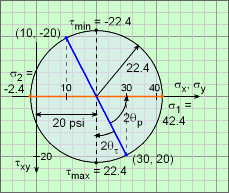 Maximum Shear Stresses and Direction |
The maximum shear stress occurs at the top or bottom of the circle. Thus, the current stress state, blue line, needs to be rotated clockwise (negative direction) by angle 2θτ. From the circle geometry, this angle is tan(-2θτ-max) = (30 - 20)/20 = 0.5 θτ-max= 13.28o The maximum shear stress (or minimum) is simply the radius of the circle which was found previously to be τmax = r = 22.36 psi |
|
|
|
||
| Arbitrary Rotation |
||
|
|
Mohr's circle can also be used to find a new stress state for an arbitrary rotation angle. The new stress state is identified by rotating the current stress state (blue line) by twice the angle, 2θ. The new stress state is shown on the diagram as a green line. Positive rotation angles are counter-clockwise. Using geometry, the stress points on the circle are σx′ = σavg + r cos(2θp - 2θ) = 20 + 22.36 cos(63.44 - 30) = 38.66 psi σy′ = σavg - r cos(2θp - 2θ) = 20 - 22.36 cos(63.44 - 30) = 1.34 psi τx′y′ = r sin(2θp - 2θ) = -22.36 sin(63.44 - 30) = 12.32 psi The initial stress state (blue line) and rotated stress state (green line) are also shown in the diagram as a small stress element to understand the orientation of the Mohr's circle stresses. |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.