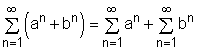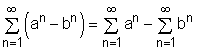| Ch 12. Infinite Sequences and Series | Multimedia Engineering Math | ||||||
|
Sequences and Series |
Integral and Comparison |
Alt. Series & Abs. Conv. |
Power Series |
Taylor, Mac. & Binomial |
|||
| Sequences and Series | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||||||||||||||
The basic concepts of sequences and its limits were briefly introduced previously. A more in-depth discussion of sequences and series will be presented in this section. |
||||||||||||||
| Sequences |
||||||||||||||
|
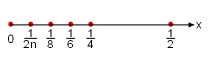
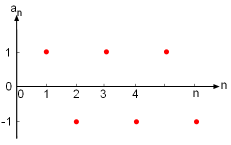
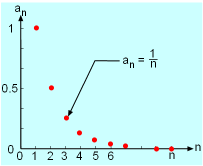
A sequence is an infinite ordered list of numbers: a1, a2, a3, ..., an where n is positive integer and an is referred to as the nth term of the sequence. It is not necessary for n to start from one. Sometimes the sequence is denoted by {an} or simply an. For example, {1, -1, 1, -1, ...} and {2, 8, 18, 32, ...} are sequences. Normally the numbers can be expressed in terms of a formula. For example, the sequence an = 3n for 1 ≤ n is {3, 6, 9, ...}. However, some sequences are random and they cannot be expressed using an equation. Sequences can be expressed using two graphical representations: (a) number line and (b) coordinate plane. Two examples of sequences are shown in the figures. Very often, as n of a sequence increases, the nth term of
the sequence approaches a particular number. Take the sequence an =
1/n for example. As n increases, an approaches 0. Hence the
limit for this sequence is 0. The formal definition of a limit is given
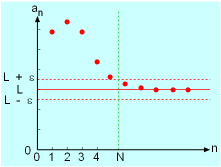
as follows: A sequence converges and is convergent if it has a finite limit. Otherwise, the sequence diverges or is said to be divergent. The figure on the left is used to further illustrate the definition. In order for a limit of a sequence to exist (or converges), the points of the sequence must lie between the lines (L + ε) and (L - ε) for n > N. Some other relations such as the limit laws and squeeze theorem may be useful in determining the limit of sequence are presented next. The limit laws for sequences were introduced in the previous section, and they are summarized without further discussion as follows: If an and bn are convergent sequences and c is an arbitrary constant, then (a) Constant Law: (f) Law of Division: Another useful relation is the squeeze theorem for a sequence: |
|||||||||||||
| Series |
||||||||||||||
When one adds the terms of an infinite sequence as follows: a1 + a2 + a3 + ... + an the above expression is referred to as an infinite series, and it is
denoted by For a series If the sequence Sn is convergent and its limit exists |
||||||||||||||
| Table: Partial Sum for a Convergent Series Σ(1/2n)
|
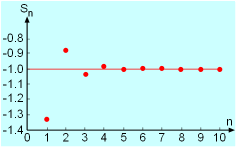
It is said that a series converges if it has a finite sum and a series
is divergent when it has an infinite sum or no sum. Take the sequence
an = 1/2n for example. As shown in the table on
the left, this series converges to 1 (i.e., Another important infinite series is the geometric series, and it is defined as |
|||||||||||||
 Geometric Series |
It is defined that the geometric series Similar to the discussion of the sequences, the following laws are applied to the series: If Σan and Σbn are convergent series and c is an arbitrary constant, then (a) Constant Law: |
|||||||||||||
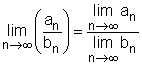 if
if 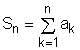 .
.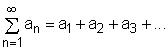 ,
and Sn is its nth partial sum
,
and Sn is its nth partial sum
 where
S is the sum of the series.
where
S is the sum of the series. ).
).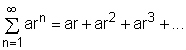
 is
convergent if
is
convergent if 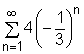 is
convergent since r = -1/3. And the geometric series is equal to -1 as shown in the figure.
is
convergent since r = -1/3. And the geometric series is equal to -1 as shown in the figure.