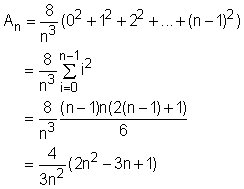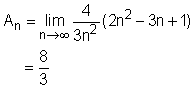| Ch 6. Integrals | Multimedia Engineering Math | ||||||
|
Indefinite Integral |
Area |
Definite Integral |
Fundamental Theorem |
Substitution Rule |
|||
| Area | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
This section introduces a method to calculate area under a curve. |
||
| Sigma Notation |
||
The Greek letter, Σ, is used to represent the sum of a series and is called sigma notation. It allows long sums (with many of terms) to be written in condensed form. In mathematics it is defined as following: If am, am+1, ... , an-1, an are real numbers and m and n are integers such that m < n, then |
||
| Rules for Sigma Notation |
||
The following formulas are some of the basic rules fro sigma notation in which c is a constant: |
||
| The sigma notation can be used in many fields of study. besides engineering, such as economics. One such application in engineering is calculating area using finite rectangular areas. | ||
| Area |
||
| In high school, the formula to calculate the area of triangle, rectangle, circle and sphere was introduced. However, some areas, such as the area under the curve y = x2, can't be calculated easily with a formula. In this case, the sigma notation can help to find the area. | ||
|
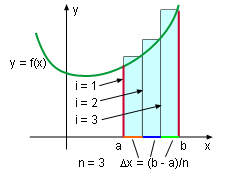
To find the area under a curve of function y = f(x) between x = a and x = b, the interval can be equally divided into n pieces. The width of each piece is Δx = (b-a)/n The left endpoint of these subintervals is xi = a + iΔx in which i = 0, 1, 2, ..., n-1. These rectangles, whose height is f(xi), are placed under the curve as shown on the left diagram. The area of each rectangle is f(xi)Δx. Therefore, the area under curve y = f(x) is approximately equal to the sum area of these rectangles. It is The more the rectangle used, the higher the accuracy is. Thus, the area can be expressed as the limit Recall, previously the left edge top corner of the rectangular area was touching the curve. Now if the right side is used, the area can be expressed with These two limits both will converge to the same value as n goes to infinite. |
|
|
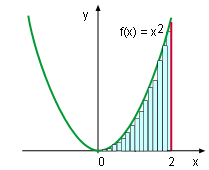
This method can be better understood by finding the area under curve y = x2 between 0 and 2. First, equally divided the interval [0, 2] into n subintervals, the width of each subinterval is 2/n. The left x coordinates of the partitions are 0/n, 2/n, 4/n, ..., 2n/n. The height of each rectangle is (xi)2. The sum of the areas of the rectangles is
|
|
 Smaller Error |
Rearranging this expression gives Taking the limit of this expression as n approaches +∞ gives the area. |
|

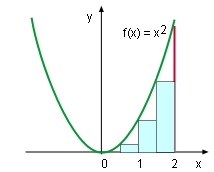 The Area Under Curve y = x2
The Area Under Curve y = x2