| Ch 4. The Mean Value Theorem | Multimedia Engineering Math | ||||||
|
Maximum & Minimum |
Rolle's Theorem |
Mean Value Theorem |
Monotonic Functions |
First Derivative Test |
Concavity & Inflection |
Second Derivative Test |
|
| Monotonic Functions | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
| In this section, the concept of a monotonic function is discussed and the method to find a function's monotonicity is introduced. | ||
| Monotonicity |
||
|
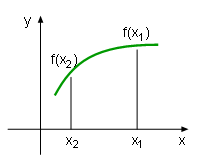
In engineering research, sometimes a diagram can help the researcher better understand a function. A function's increasing or decreasing tendency is useful when sketching a draft. A function is called increasing on an interval if the function value increases as the independent value increases. That is if x1 > x2, then f(x1) > f(x2). On the other hand, a function is called decreasing on an interval if the function value decreases as the independent value increases. That is if x1 > x2, then f(x1) < f(x2). A function's increasing or decreasing tendency is called monotonicity on its domain. |
|
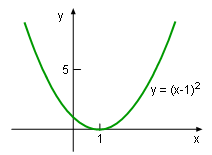 Example of Monotonic Function |
The monotonicity concept can be better understood by finding the increasing and decreasing interval of the function, say y = (x-1)2. In the interval of (-∞, 1], the function is decreasing. In the interval of [1, +∞), the function is increasing. However, the function is not monotonic in its domain (-∞, +∞). |
|
|
|
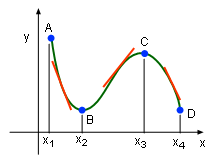
In the Derivative and Monotonic graphic on the left, the function is decreasing in [x1, x2] and [x3, x4], and the slope of the function's tangent lines are negative. On the other hand, the function is increasing in [x2, x3] and the slope of the function's tangent line is positive. Is there any certain relationship between monotonicity and derivative? The answer is yes and is discussed below. |
|
| Test for Monotonic Functions |
||
|
Test for monotonic functions states: Suppose a function is continuous on [a, b] and it is differentiable on (a, b).
|
||
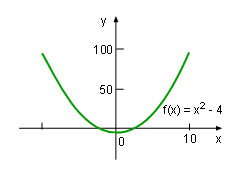 Function y = x2 - 4 |
The test for monotonic functions can be better understood by finding the increasing and decreasing range for the function f(x) = x2 - 4. The function f(x) = x2 - 4 is a polynomial function, it is continuous and differentiable in its domain (-∞, +∞), and thus it satisfies the condition of monatomic function test. In order to find its monotonicity, the derivative of the function needs to be calculated. That is df(x)/dx = d(x2 - 4)/dx = (d(x2) - d(4))/dx = 2x It is obvious that the function df(x)/dx = 2x is negative when x < 0, and it is positive when x > 0. Therefore, function f(x) = x2 - 4 is increasing in the range of (-∞, 0) and decreasing in the range of (0, +∞). This result is confirmed by the diagram on the left. |
|