| Ch 2. Derivatives I | Multimedia Engineering Math | ||||||
|
Derivative Formulas |
Trigonometric Functions |
Differentiability |
Chain Rule |
Implicit Differentiation |
|||
| Implicit Differentiation | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
|
In the last section, the Chain Rule is introduced. It can calculate the derivative of a function when it is can be expressed in terms of another expression, such as y = (x +1)2 sin(x + 1).
|
|
 Implicit Differentiation Example |
Suppose y is defined by a relation with x and it is hard to express the function y in terms of x. For example, x3 + y3 - 4xy = 0. In order to draw the diagram of function x3 + y3 - 4xy = 0, the diagram of function z = x3 + y3 - 4xy is plotted. The function z intersects the x-y plane at z = 0. The function expression and diagram shows that y is hard to be rewritten in term of x. In these cases, the derivative of y can be calculated by with the Implicit Differentiation method. | |
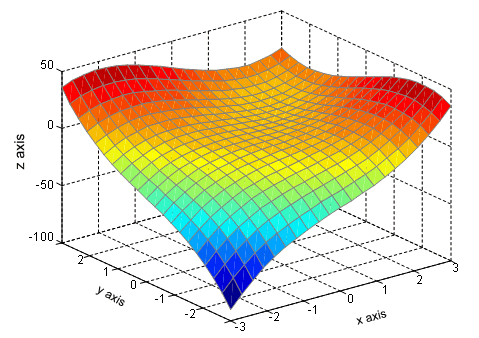 Function z = x3 + y3 - 4xy |
||
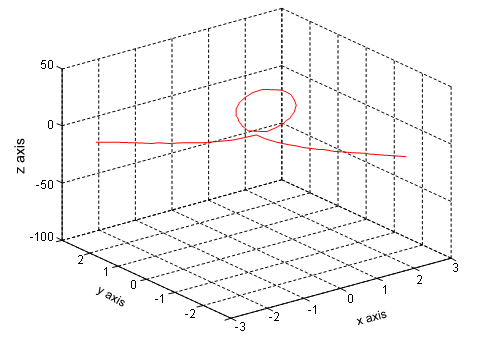 Function x3 + y3 - 4xy = 0 |
||
| Implicit Differentiation |
||
 Implicit Differentiation |
The implicit differentiation method states: An equation f(x,y) = 0 defines y implicitly as a function of x. In order to to find the derivative of y, differentiate both sides of the original equation f(x, y) = 0 and solve the resulting equation for dy/dx. This differentiation method is known as implicit differentiation. For example, given x3 + y3 - 4xy = 0, find dy/dx. Differentiate both side of x3 + y3 - 4xy = 0 with respect to x, gives Since y is implicitly defined by x, d(y3)/dx is not 0. Consider z = y3 and apply Chain Rule, Recall that if F(x) = f(x)g(x), then F '(x) = f '(x)g(x) + f (x)g '(x).The formula can be used to calculate d(4xy)/dx. Consider f(x) = x and g(x) = y, thus Substitute equation(2) and (3) into (1), so 3x2 + 3y2dy/dx - (4y + 4xdy/dx) = 0 (3y2 - 4x)dy/dx = 4y - 3x2 dy/dx = (4y - 3x2)/(3y2 - 4x) |
|

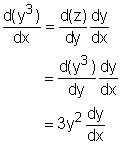 (2)
(2)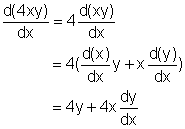 (3)
(3)