| Ch 2. Derivatives I | Multimedia Engineering Math | ||||||
|
Derivative Formulas |
Trigonometric Functions |
Differentiability |
Chain Rule |
Implicit Differentiation |
|||
| Implicit Differentiation | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| MATHEMATICS - CASE STUDY SOLUTION |
||
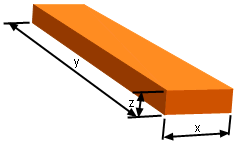 Rectangular Box |
Recall Tony made a rectangular box with 100 in2 surface
area in his arts and crafts class. The length of his box is 3 times of
its width. He wondered how the height changes affects width's enlargement? Let the surface area of the box be s. The surface area of the box can be calculated as s = 2xy + 2xz + 2yz Since the length is 3 times of the box's width, substitute y = 3x into the equation. s = 2x(3x) + 2xz + 2z(3x) = 6x2 + 2xz + 6zx = 6x2 + 8xz Because the height z is implicitly defined by its width x, the expression, the height z changes with respect to its width x (dz/dz), can be calculated using implicit differentiation method. Differentiate both side of surface area equation with respect to x ds/dx = d(6x2 + 8xz)/dx The left hand side of the equation, ds/dx is zero since the surface area is constant at 100 in2. The right hand side is The left hand side equals the right hand side, so 12x + 8z + 8xdz/dx = 0 Rearranging gives dz/dx = -(3x + 2z)/2x = -1.5 + z/x |
|