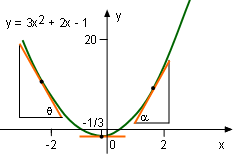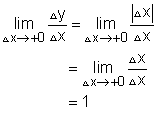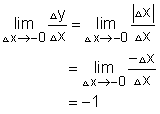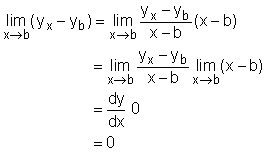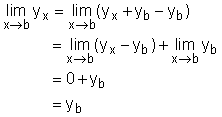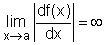| Ch 2. Derivatives I | Multimedia Engineering Math | ||||||
|
Derivative Formulas |
Trigonometric Functions |
Differentiability |
Chain Rule |
Implicit Differentiation |
|||
| Differentiability | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
MATHEMATICS - CASE STUDY SOLUTION |
||
| Although there are situations when a function cannot be differentiated, the discussion in this sectionfocuses on the function's differentiability. | ||
| Differentiable |
||
|
Consider for example, the function y = 3x2 + 2x - 1, then dy/dx = 6x + 2, which is reasonable. When x < -1/3, dy/dx or tanθ is negative and when x > -1/3, dy/dx or tanα is positive. When x= 1/3, the slope of the tangent line is horizontal and thus equal to 0. These correspond to its derivative function figure and it is obvious that the function is differentable at all points. |
|
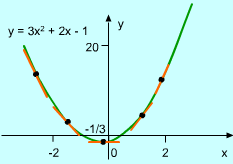 3x2 + 2x - 1 is differentiable |
A function is differentiable at a point if the derivative of the function exists at that point. A function is differentiable on an interval if it is differentiable at every point in the interval, as already concluded. According to the above definition, y = 3x2 + 2x - 1 function is differentiable. |
|
|
|
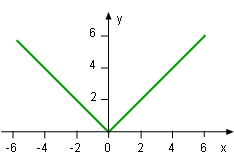
Now, consider another example, y = (x2)0.5. Is y differentiable in this case at all points? The definition of derivative gives At x = 0, The left hand limit is: The right hand limit is: The left hand limit is not equal to the right hand limit. Thus |
|
| Differentiability and Continuity |
||
If a function is differentiable at point b, then this function is continuous at this specific point. proof: When x approaches b, the difference between f(x) and f(b) is yx - yb. Since x ≠ b, yx - yb can be written as: Thus |
||
|
|
Therefore, This proves that when y is differentiable at point b, it is continuous at that point. Function y = 3x2 + 2x - 1 is differentiable in its variable range, and so it is continuous. If a function is continuous, is it differentiable? The answer is may not be. For example y = (x2)0.5 is continuous, but it was shown that it is not differentiable. |
|
| Differentiability and Continuity |
||
|
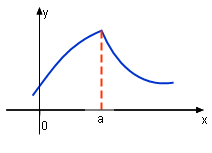
Function y = (x2)0.5 is not differentiable at 0 because its left hand limit is not equal to its right hand limit. Normally, if a function's graphic has a corner or kink (loop), then the function is not differentiable.
|
|
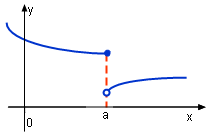 Not Differentiable at a -- Function Discontinuous |
If a function's graphic is discontinuous, then this function is not differentiable. since the function's left and right hand limits are different. | |
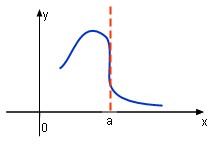 Not Differentiable at a -- Vertical Tangent Line |
When the curve of a continuous function has a vertical tangent line at point a, the slope of the tangent line is infinity. This means Thus the function is not differentiable. |
|