| Ch 2. Derivatives I | Multimedia Engineering Math | ||||||
|
Derivative Formulas |
Trigonometric Functions |
Differentiability |
Chain Rule |
Implicit Differentiation |
|||
| Differentiability | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| MATHEMATICS - CASE STUDY SOLUTION |
||
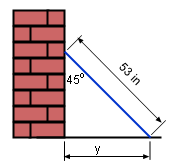 Tilt ice Hockey Stick |
A 53 in ice hockey stick rests against a vertical wall. The bottom of the stick slides away from the wall. How fast does the distance, y change with respect to the angle, θ, which is made by the wall and the stick, when θ is equals 45o?
|
|
|
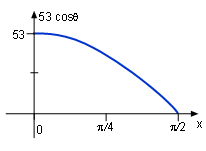
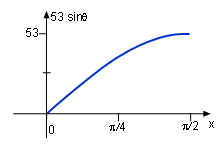
According to the diagram, sinθ = y/53 Thus y = 53 sinθ Derivative y with respect to θ dy/dθ = d(53 sinθ)/dθ =53 cosθ When θ = 45o, dy/dθ = 53 cosθ = 37.5 in/rad The derivative of y = 53 sinθ is dy/dθ = 53 cosθ when θ is in the range of (0, π/2). Since y is differentiable, it is continuous, this is shown in the plot of y = 53 sinθ. |
|