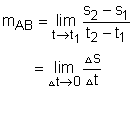| Ch 1. Limits | Multimedia Engineering Math | ||||||
|
Limit of a Sequence |
Limit of a Function |
Limit Laws |
Continuity |
Rate Change |
|||
| Rate Change | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
| Slope of a line |
||
 Slope of a Line |
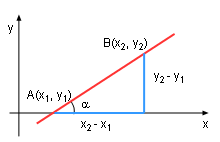
The slope of a line is denoted by m and can be determined with two points: A(x1,y1) and B(x2, y2). It can also be determined by: in which α is the smallest positive angle from the x axis to the line. When the line is horizontal, m = 0 and when the line is vertical, m is infinity or not defined. |
|
|
||
| Tangent |
||
 Slope of a Curve |
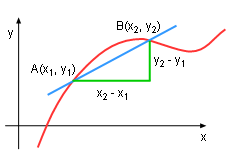
Suppose curve C (f(x)) is a function of x, the tangent line of the curve C at point A is desired. Now, consider B point where x2 is not equal to x1, the slope of AB is: |
|
 Tangent of a Curve |
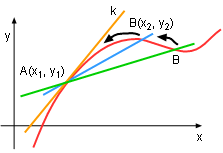
Let point B approaches A along the curve C by letting x2 approaches x1, when x2 - x1 is small enough, the slope of AB will overlap with its tangent line at point A.Thus, the tangent at point A can be written as: |
|
| Tangent Example - Velocity |
||
Velocity is a good example of a tangent line. Normally, the distance s is a function of time t. The velocity of a time interval is |
||
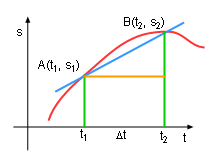 Velocity of any Function |
On a graph of distance plotted as a function of time, the tangent (instantaneous velocity) is: Therefore, the instantaneous velocity at time t, is equal to the slope of the tangent line at point A. |
|