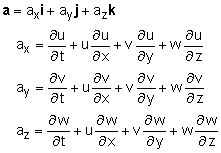| Ch 3. Fluid Kinematics | Multimedia Engineering Fluids | ||||||
|
Flow Descriptions |
Steady & Unsteady |
Streamlines, Streaklines |
Velocity & Acceleration |
Irrotational Flow |
|||
| Velocity and Acceleration Fields | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
Two basic and important field variables in the study of fluid mechanics are the velocity and acceleration of the fluid, and they are the focus of the discussion in this section. Both the velocity and acceleration equations are presented in Eulerian viewpoint. |
|||||
| Velocity Field |
|||||
|
|
Velocity is an important basic parameter governing a flow field. Other field variables such as the pressure and temperature are all influenced by the velocity of the fluid flow. In general, velocity is a function of both the location and time. The velocity vector can be expressed in Cartesian coordinates as
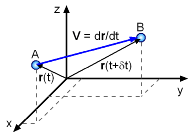
where the velocity components (u, v and w) are functions of both position and time. That is, u = u(x, y, z, t), v = v(x, y, z, t) and w = w(x, y, z, t). This velocity description is called the velocity field since it describes the velocity of all points, Eulerian viewpoint, in a given volume. For a single particle, Lagrangian viewpoint, the velocity is derived from the changing position vector, or V = dr/dt = = dx/dt i + dy/dt j + dz/dt k where r is the position vector (r = xi + yj + zk). Notice, the velocity is only a function of time since it is only tracking a single particle. |
||||
| Acceleration Field |
|||||
|
|
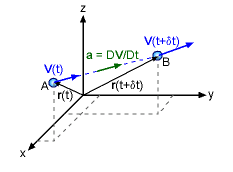
Another important parameter in the study of fluid in motion is the acceleration. Acceleration is related to the velocity, and it can be determined once the velocity field is known. The acceleration is the change in velocity, δV, over the change in time, δt, a = [dV(t + δ) - dV(t)] / δt = δV/δt = dV/dt But it is not just a simple derivative of just time since the velocity is a function time, AND space (x,y,z). The change in velocity must be track in both time and space. Using the chain rule of calculus, the change in velocity is, This can simplified using u, v, and w, the velocity magnitudes in the three coordinate directions. In cartesian coordinates, the acceleration field is This expression can be expanded and rearranged as The acceleration equation can also be written in polar coordinates and are given in the Basic Equations appendix. |
||||
| Material Derivative |
|||||
The time and space derivative used to determine the acceleration field from the velocity is so common in fluid mechanics, it has a special name. It is called the Material or Substantial Derivative and has a special symbol, D( )/Dt. For cartesian coordinates, it is or in vector form, where The second term, As an example, the acceleration field equation can be written as |
|||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.