| Ch 3. Fluid Kinematics | Multimedia Engineering Fluids | ||||||
|
Flow Descriptions |
Steady & Unsteady |
Streamlines, Streaklines |
Velocity & Acceleration |
Irrotational Flow |
|||
| Flow Descriptions | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
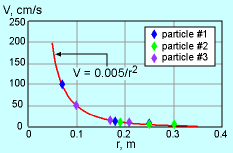
Since it is given that the velocity is inversely proportional to the square of the location r, assume the correlation for velocity has the following form: V = c/r2 where c is a constant which needs to be determined. |
|||||||||||||||||||||||||||||||||||||||||||||||||
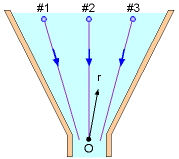
 Schematic of Experiment Set #1 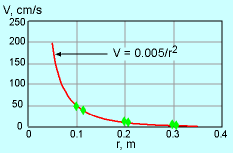 Correlation for Experiment Set #1 |
For experiment set #1, the locations of the measurement points are first determined (using the Pythagorean theorem):
By taking the average of the calculated values for the constant c, it is found that c is 0.00497, which is close to 0.005. The Eulerian viewpoint is used in this experiment since the velocities are measured at fixed locations. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
For experiment set #2:
The average value for the constant c is 0.00498, which is again close to 0.005. Since the measurements in set #2 are taken by following individual fluid particles, the flow field is determined using the Lagrangian viewpoint. |
|||||||||||||||||||||||||||||||||||||||||||||||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.